某工厂对某产品的产量与单位成本的资料分析后有如下数据:
| 月 份 |
1 |
2 |
3 |
4 |
5 |
6 |
| 产量x千件 |
2 |
3 |
4 |
3 |
4 |
5 |
| 单位成本y元/件 |
73 |
72 |
71 |
73 |
69 |
68 |
(Ⅰ)求单位成本y与月产量x之间的线性回归方程.(其中已计算得: ,结果保留两位小数)
,结果保留两位小数)
(Ⅱ)当月产量为12千件时,单位成本是多少?
已知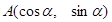 .
. ,其中
,其中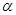 、
、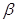 为锐角,且
为锐角,且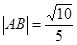 .
.
(1)求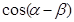 的值;
的值;
(2)若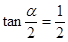 ,求
,求 及
及 的值.
的值.
如图在长方体 中,
中, ,
,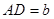 ,
,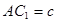 ,点
,点 为
为 的中点,点
的中点,点 为
为 的中点.
的中点.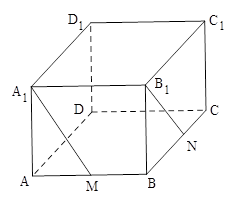
(1)求长方体 的体积;
的体积;
(2)若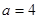 ,
, ,
, ,求异面直线
,求异面直线 与
与 所成的角.
所成的角.
已知函数 ,
,
(Ⅰ)当a=4时,求函数f(x)的单调区间;
(Ⅱ)求函数g(x)在区间 上的最小值;
上的最小值;
(Ⅲ)若存在 ,使方程
,使方程
 成立,求实数a的取值范围(其中e=2.71828是自然对数的底数)
成立,求实数a的取值范围(其中e=2.71828是自然对数的底数)
已知椭圆C: 的离心率为
的离心率为 ,长轴长为
,长轴长为 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线 交椭圆C于A、B两点,试问:在y轴正半轴上是否存在一个定点M满足
交椭圆C于A、B两点,试问:在y轴正半轴上是否存在一个定点M满足 ,若存在,求出点M的坐标;若不存在,请说明理由.
,若存在,求出点M的坐标;若不存在,请说明理由.
设正项数列 an
an 为等比数列,它的前n项和为Sn,a1=1,且
为等比数列,它的前n项和为Sn,a1=1,且 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)已知 是首项为1,公差为2的等差数列,求数列
是首项为1,公差为2的等差数列,求数列 的前n项和Tn.
的前n项和Tn.