已知抛物线y=ax2+bx+3与y轴的交点为A,点A与点B关于抛物线的对称轴对称,二次函数y=ax2+bx+3的y与x的部分对应值如下表:
| x |
… |
﹣1 |
0 |
1 |
3 |
4 |
… |
| y |
… |
8 |
|
0 |
0 |
|
… |
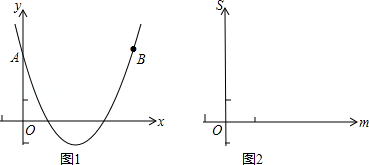
(1)抛物线的对称轴是_________ .点A(______,____),B(_____,_____);
(2)求二次函数y=ax2+bx+3的解析式;
(3)已知点M(m,n)在抛物线y=ax2+bx+3上,设△BAM的面积为S,求S与m的函数关系式、画出函数图象.并利用函数图象说明S是否存在最大值,为什么?
如图所示在平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE= CD.
CD.
(1)求证:△ABF∽△CEB;
(2)若S△DEF面积为2,求S平行四边形ABCD的面积。
已知 ,求
,求 。
。
在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,表是活动进行中的一组统计数据:
| 摸球的次数n |
100 |
150 |
200 |
500 |
800 |
1000 |
| 摸到白球的次数m |
68 |
109 |
136 |
345 |
368 |
701 |
| 摸到乒乓球的频率 |
0.68 |
0.73 |
0.68 |
0.69 |
0.70 |
0.70 |
(1)请估计:当n很大时,摸到白球的频率将会接近________;
(2)假如你去摸一次,你摸到白球的概率是_______,摸到黑球的概率是_______;
(3)试估算口袋中黑、白两种颜色的球各有多少只?
如图,正方形ABCD中,E、F分别是AB、BC边上的点,且AE=BF,求证:AF⊥DE。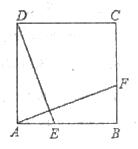
用适当的方法解下列方程
(1) (2)
(2)