已知:AB是⊙O的直径,弦CD⊥AB于点G,E是直线AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P.设⊙O的半径为r.
(1)如图1,当点E在直径AB上时,试证明:OE·OP=r2
(2)当点E在AB(或BA)的延长线上时,以如图2点E的位置为例,请你画出符合题意的图形,标注上字母,(1)中的结论是否成立?请说明理由.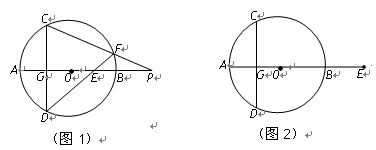
某玩具厂授权生产工艺品福娃,每日最高产量为30只,且每日生产的产品全部出售.已知生产 只福娃的成本为
只福娃的成本为 (元),每只售价
(元),每只售价 (元),且
(元),且 ,
, 与
与 的表达式分别为
的表达式分别为 ,
, .当日产量为多少时,可获得最大利润?最大利润是多少?
.当日产量为多少时,可获得最大利润?最大利润是多少?
(本题满分10分)
已知:等腰三角形OAB在直角坐标系中的位置如图,点A的坐标为( ),点B的坐标为(-6,0).
),点B的坐标为(-6,0).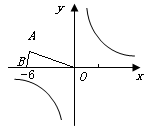
(1)若△OAB关于y轴的轴对称图形是三角形O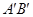 ,请直接写出A、B的对称点
,请直接写出A、B的对称点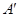
 的坐标;
的坐标;
(2)若将△ 沿x轴向右平移a个单位,此时点A恰好落在反比例函数
沿x轴向右平移a个单位,此时点A恰好落在反比例函数 的图像上,求a的值.
的图像上,求a的值.
(本题满分8分)
某隧道横断面由抛物线与矩形的三边组成,尺寸如图所示,某卡车空车时能通过此隧道,现装载一集装箱箱宽3 ,车与箱共高4.5
,车与箱共高4.5 ,此车能否通过此隧道?
,此车能否通过此隧道?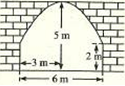
(本题满分8分)
已知扇形的圆心角为1200,面积为300πcm2.
(1)求扇形的弧长;
(2)若把此扇形卷成一个圆锥,则这个圆锥的轴截面面积是多少?