如图，在△ABC中，∠ACB=90°，AC=BC，点D在边AB上，连接CD，将线段CD绕点C顺时针旋转90°至CE位置，连接AE．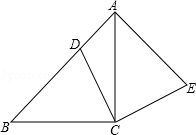
（1）求证：AB⊥AE；
（2）若BC2=AD•AB，求证：四边形ADCE为正方形
如图，已知A（-4，2）、B（n，-4）是一次函数y=kx+b的图象与反比例函数
的图象的两个交点． 
（1）求此反比例函数和一次函数的解析式；
（2）根据图象写出使一次函数的值小于反比例函数的值的x的取值范围．
一船在A处测得北偏东60°方向有一灯塔B，船向正东方向以每小时20海里的速度航行1.5小时到达C处时，又观测到灯塔B在北偏东15°方向上，求此时航船与灯塔相距多少海里?
如图是由4个边长为1的正方形组成的图形，请求出∠ABC的度数。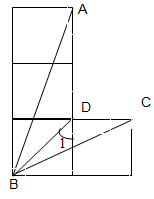
维修人员为更换一圆柱形的输水管道，需先确定管道圆形截面的半径，下图是水平放置的破裂管道有水部分的截面，若这个输水管道有水部分的水面宽AB=16cm，水面最深地方的高度为4cm，求这个圆形截面的半径.