如图,平面上有四个点A、B、C、D,根据下列语句画图.
(1)画直线AB;
(2)作射线BC;
(3)画线段CD;
(4)连接AD,并将其反向延长至E,使DE=2AD;
(5)找到一点F,使点F到A、B、C、D四点距离和最短.
如图,梯形ABCD中,AB∥DC,AC平分∠BAD,CE∥DA交AB于点E.求证:四边形ADCE是菱形.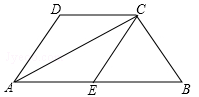
如图,为测量某建筑物BC上旗杆AB的高度,小明在距离建筑物BC底部11.4米的点F处,测得视线与水平线夹角∠AED=60°,∠BED=45°.小明的观测点与地面的距离EF为1.6米.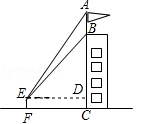
(1)求建筑物BC的高度;
(2)求旗杆AB的高度(结果精确到0.1米).
参考数据: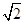 ≈1.41,
≈1.41,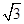 ≈1.73.
≈1.73.
先化简再求值: ,其中
,其中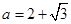 .
.
已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.
(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
如图,四边形ABCD是边长为2,一个锐角等于60°的菱形纸片,小芳同学将一个三角形纸片的一个顶点与该菱形顶点D重合,按顺时针方向旋转三角形纸片,使它的两边分别交CB、BA(或它们的延长线)于点E、F,∠EDF=60°,当CE=AF时,如图1小芳同学得出的结论是DE=DF.
(1)继续旋转三角形纸片,当CE≠AF时,如图2小芳的结论是否成立?若成立,加以证明;若不成立,请说明理由;
(2)再次旋转三角形纸片,当点E、F分别在CB、BA的延长线上时,如图3请直接写出DE与DF的数量关系;
(3)连EF,若△DEF的面积为y,CE=x,求y与x的关系式,并指出当x为何值时,y有最小值,最小值是多少?