如图,在水平轨道右侧固定半径为R的竖直圆槽形光滑轨道,水平轨道的PQ段铺设特殊材料,调节其初始长度为l,水平轨道左侧有一轻质弹簧左端固定,弹簧处于自然伸长状态.可视为质点的小物块从轨道右侧A点以初速度v0冲上轨道,通过圆形轨道、水平轨道后压缩弹簧,并被弹簧以原速率弹回.已知R=0.4m,l=2.5m,v0=6m/s,物块质量m=1kg,与PQ段间的动摩擦因数μ=0.4,轨道其它部分摩擦不计.取g=10m/s2.求:
(1)物块经过圆轨道最高点B时对轨道的压力;
(2)物块从Q运动到P的时间及弹簧获得的最大弹性势能;
(3)物块仍以v0从右侧冲上轨道,调节PQ段的长度l,当l长度是多少时,物块恰能不脱离轨道返回A点继续向右运动.
如图所示,一质量为m=1.0×10-2 kg、带电荷量为q=1.0×10-6 C 的小球,用绝缘细线悬挂在水平向右的匀强电场中,假设电场足够大,静止时悬线向左与竖直方向成60°角。小球在运动过程中电荷保持不变,重力加速度取g=10 m/s2。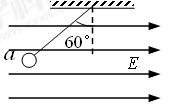
(1)判断小球带何种电荷;
(2)求电场强度E的大小;
(3)若在某时刻将细线突然剪断,求小球运动的加速度a。
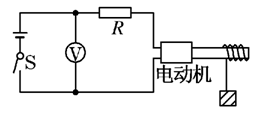
如图所示,直流电动机提升重物,重物的质量m=50kg,电源供电电压为110V,不计各处摩擦,当电动机以v=0.90m/s的恒定速度向上提升重物时,电路中的电流为5A,求:
(1)电动机输出的机械功率为多少?
(2)电动机线圈的电阻为多大?
受动画片《四驱兄弟》的影响,越来越多的小朋友喜欢上了玩具赛车.某玩具赛车充电电池的输出功率P随电流I变化的图象如图所示。
(1)求该电池的电动势E和内阻r;
(2)求该电池的输出功率最大时对应的外电阻R(纯电阻);
(3)由图象可以看出,同一输出功率P可对应两个不同的电流I1、I2,即对应两个不同的外电阻(纯电阻)R1、R2,试确定r、R1、R2三者间的关系。
如图甲所示电路中,电源电动势E=12V,内阻r=2Ω,R1=4Ω,R2=6Ω,R3=3Ω。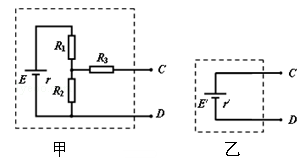
(1)图甲中虚线框内的电路可等效为一个电源,即图甲可等效为图乙,其等效电动势E′等于CD间未接入用电器时CD间的电压;若用导线直接将CD两点连接起来,通过该导线的电流等于等效电源的短路电流,则等效电源的内电阻r′是多少?
(2)若在C、D间连一个“6V,3W”的小灯泡,则小灯泡的实际功率是多少?(不考虑小灯泡的电阻率随温度的变化)
利用电动机通过如图所示的电路提升重物,已知电源电动势E=6 V,电源内阻r=1 Ω,电阻R=3 Ω,重物质量m=0.10 kg,当将重物固定时,电压表的示数为5 V,当重物不固定,且电动机最后以稳定的速度匀速提升重物时,电压表的示数为5.5 V,求重物匀速上升时的速度大小(不计摩擦,g取10 m/s2)。