设△ABC的内角A、B、C所对边的长分别为a、b、c，且有2sinBcosA=sinAcosC+cosAsinC．
（Ⅰ）求角A的大小；
（Ⅱ）若b=2，c=1，D为BC的中点，求AD的长．
(本题满分12分)
已知A=
，设
，试比较
与
的大小.
(本题满分10分)
已知
是奇函数
⑴、求
的定义域；
⑵、求
的值；
（本小题满分15分）已知函数
（1）若函数
在
上为增函数，求正实数
的取值范围;
（2）当
时，求在
上的最大值和最小值;
（3）当时，求证：对大于1的任意正整数
，都有
（本小题满分15分） 已知点P是
上的任意一点，过P作PD
垂直x轴于D,动点Q满足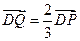
.
（1）求动点Q的轨迹方程;
（2）已知点E(1,1)，在动点Q的轨迹上是
否存在两个不重合的两点M、N，
使
(O
是坐标原点)，若存在，求出直线MN的方程，
若不存在，请说明理由。
(本小题满分14分)
在四棱锥P—ABCD中，底面ABCD是一直角梯形，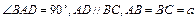
，
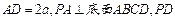与底面成30°角.
（1）若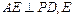
为垂足，求证：
;
（2）求平面PAB与平面PCD所成的锐二面角的余弦值.