(本小题满分15分) 已知点P是 上的任意一点,过P作PD
上的任意一点,过P作PD
垂直x轴于D,动点Q满足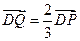 .
.
(1)求动点Q的轨迹方程;
(2)已知点E(1,1),在动点Q的轨迹上是 否存在两个不重合的两点M、N,
否存在两个不重合的两点M、N,
使 (O
(O 是坐标原点),若存在,求出直线MN的方程,
是坐标原点),若存在,求出直线MN的方程,
若不存在,请说明理由。
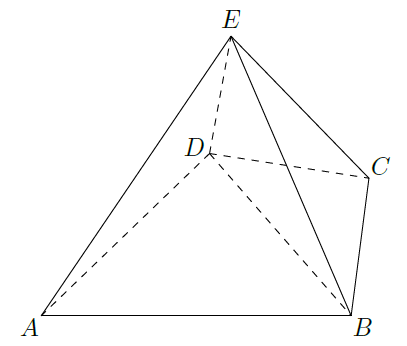
如图,几何体
是四棱锥,
为正三角形,
.
(Ⅰ)求证:
;
(Ⅱ)若
,
为线段
的中点,求证:
平面
.
袋中有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.
(Ⅰ)从以上五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率;
(Ⅱ)现袋中再放入一张标号为0的绿色卡片,从这六张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率.
在
中,内角
所对的边分别为
,已知
.
(Ⅰ)求证:
成等比数列;
(Ⅱ)若
,求
的面积
.
已知函数
.
(Ⅰ)当
时,求不等式
的解集;
(Ⅱ) 若
的解集包含
,求
的取值范围.
已知曲线
的参数方程是
(
是参数),以坐标原点为极点,
轴的正半轴为极轴建立极坐标系,曲线
:的极坐标方程是
,正方形
的顶点都在
上,且
依逆时针次序排列,点
的极坐标为
.
(Ⅰ)求点
的直角坐标;
(Ⅱ)设P为
上任意一点,求
的取值范围.