已知抛物线C: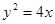 ,P为C上一点且纵坐标为2,Q,R是C上的两个动点,且
,P为C上一点且纵坐标为2,Q,R是C上的两个动点,且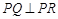 .
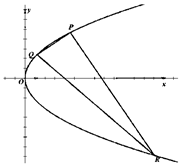
.
(1)求过点P,且与C恰有一个公共点的直线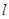 的方程;
的方程;
(2)求证:QR过定点.
(本小题满分10分)【选修4-5:不等式选讲】
设函数 (
( ).
).
(Ⅰ)证明: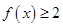 ;
;
(Ⅱ)若 ,求
,求 的取值范围.
的取值范围.
(本小题满分10分)【选修4-4:坐标系与参数方程】
已知圆的参数方程为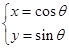 (
( ,
,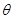 为参数),将圆上所有点的横坐标伸长到原来的
为参数),将圆上所有点的横坐标伸长到原来的 倍,纵坐标不变得到曲线
倍,纵坐标不变得到曲线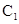 ;以坐标原点为极点,以
;以坐标原点为极点,以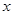 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.
(Ⅰ)求曲线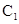 的普通方程与曲线
的普通方程与曲线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设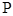 为曲线
为曲线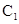 上的动点,求点
上的动点,求点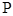 与曲线
与曲线 上点的距离的最小值,并求此时
上点的距离的最小值,并求此时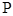 点的坐标.
点的坐标.
(本小题满分10分)【选修4-1:几何证明选讲】
如图,已知圆上的弧 ,过点
,过点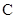 的圆的切线
的圆的切线 与
与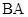 的延长线交于
的延长线交于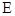 点.
点.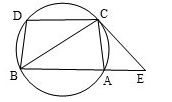
求证:(Ⅰ)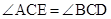 ;
;
(Ⅱ) .
.
(本小题满分12分)已知函数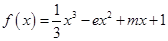 ,
,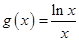 .
.
(Ⅰ)函数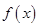 在点
在点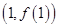 处的切线与直线
处的切线与直线 平行,求函数
平行,求函数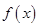 的单调区间;
的单调区间;
(Ⅱ)设函数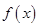 的导函数为
的导函数为 ,对任意的
,对任意的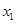 ,
,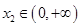 ,若
,若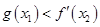 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本题小满分12分)已知椭圆
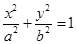 (
(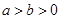 )的一个焦点与抛物线
)的一个焦点与抛物线 的焦点重合,椭圆
的焦点重合,椭圆 上一点到其右焦点
上一点到其右焦点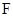 的最短距离为
的最短距离为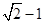 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)记椭圆 的上顶点为
的上顶点为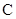 ,是否存在直线
,是否存在直线 交椭圆
交椭圆 于
于 ,
, 两点,使点
两点,使点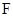 恰好为
恰好为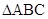 的垂心?若存在,求出直线
的垂心?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.