某学生参加3个项目的体能测试,若该生第一个项目测试过关的概率为 ,第二个项目、第三个项目测试过关的概率分别为x,y(
,第二个项目、第三个项目测试过关的概率分别为x,y( ),且不同项目是否能够测试过关相互独立,记
),且不同项目是否能够测试过关相互独立,记 为该生测试过关的项目数,其分布列如下表所示:
为该生测试过关的项目数,其分布列如下表所示:
(1)求该生至少有2个项目测试过关的概率;
(2)求 的数学期望
的数学期望 .
.
(1)若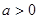 ,
,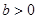 ,求证:
,求证: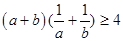 ;
;
(2)已知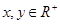 ,且
,且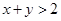 , 求证:
, 求证: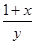 与
与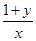 中至少有一个小于2.
中至少有一个小于2.
已知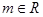 ,设
,设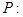
 和
和 是方程
是方程 的两个根,不等式
的两个根,不等式 对任意实数
对任意实数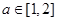 恒成立;
恒成立; 函数
函数 有两个不同的零点.求使“P且Q”为真命题的实数
有两个不同的零点.求使“P且Q”为真命题的实数 的取值范围.
的取值范围.
为了比较注射A,B两种药物后产生的皮肤疱疹的面积,选200只家兔做实验,将这200只家兔随机地分成两组。每组100只,其中一组注射药物A,另一组注射药物B。下表1和表2分别是注射药物A和药物B后的实验结果。(疱疹面积单位: )
)
表1:注射药物A后皮肤疱疹面积的频数分布表
| 疱疹面积 |
 |
 |
 |
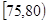 |
| 频数 |
30 |
40 |
20 |
10 |
| 频率/组距 |
表2:注射药物B后皮肤疱疹面积的频数分布表
| 疱疹面积 |
 |
 |
 |
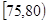 |
 |
| 频数 |
10 |
25 |
20 |
30 |
15 |
| 频率/组距 |
(1)完成上面两个表格及下面两个频率分布直方图;
(2)完成下面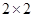 列联表,并回答能否有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”。 (结果保留4位有效数字)
列联表,并回答能否有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”。 (结果保留4位有效数字)
疱疹面积小于70 |
疱疹面积不小于70 |
合计 |
|
| 注射药物A |
a= |
b= |
|
| 注射药物B |
c= |
d= |
|
| 合计 |
n= |
附:
| P(K2≥k) |
0.10 |
0.05 |
0.025 |
0.010 |
0.001 |
| k |
2.706 |
3.841 |
5.024 |
6.635 |
10.828 |
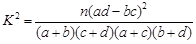 ;
;
已知集合A=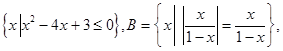
 ,
,
且 ,求
,求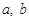 的值。
的值。
已知复数 ,若
,若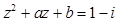 ,
,
⑴求 ;⑵求实数
;⑵求实数 的值.
的值.