据电力部门统计,每天8:00至21:00是用电的高峰期,简称“峰时”,21:00至次日8:00是用电的低谷时期,简称“谷时”,为了缓解供电需求紧张矛盾,某市电力部门于本月初统一换装“峰谷分时”电表,对用电实行“峰谷分时电价”新政策,具体见下表:
| 时间 |
换表前 |
换表后 |
|
| 峰时(8:00~21:00) |
谷时(21:00~次日8:00) |
||
| 电价 |
每度0.52元 |
每度0.55元 |
每度0.30元 |
(1)小张家上月“峰时”用电50度,“谷时”用电20度,若上月初换表,则相对于换表前小张家的电费是增多了还是减少了?增多或减少了多少元?请说明理由.
(2)小张家这个月用电95度,经测算比换表前使用95度电节省了5.9元,问小张家这个月使用“峰时电”和“谷时电”分别是多少度?
(本题满分20分,每小题5分)计算:
(1)a2•a4+(﹣a2)3
(2)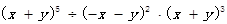
(3)(-3)0+( )-1+(-2)3×2-4
)-1+(-2)3×2-4
(4)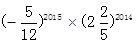
已知,如图在平面直角坐标系中,S△ABC=30,∠ABC =450,BC=12,求△ABC三个顶点的坐标.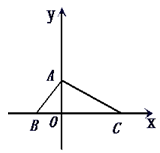
(1)如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠B=900,△ACD是直角三角形吗?为什么?
(2)小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问铺满这块空地共需花费多少元?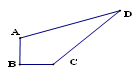
如图,将长为2.5米长的梯子AB斜靠在墙上,BE长0.7米。
(1)求梯子上端到墙的底端E的距离(即AE的长);
(2)如果梯子的顶端A沿墙下滑0.4米(即AC=0.4米),则梯脚B将外移(即BD长)多少米?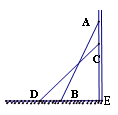
如图,如果□ABCD的一内角∠BAD的平分线交BC于点E,且AE=BE,求□ABCD各内角的度数.