某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)当销售单价为70元时,每天的销售利润是多少?
(2)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式,并求出自变量 的取值范围;
的取值范围;
(3)如果该企业每天的总成本不超过7000元,那么销售单价为多少元时,每天的销售利润最大?最大利润是多少?(每天的总成本=每件的成本×每天的销售量)
如图,抛物线y=ax2+bx﹣4与x轴交于A(4,0)、B(﹣2,0)两点,与y轴交于点C,点P是线段AB上一动点(端点除外),过点P作PD∥AC,交BC于点D,连接CP.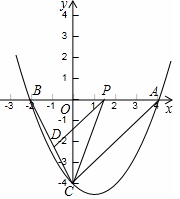
(1)求该抛物线的解析式;
(2)当动点P运动到何处时,BP2=BD•BC;
(3)当△PCD的面积最大时,求点P的坐标.
如图1,已知Rt△ABC中,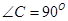 ,AC=8cm,BC=6cm.点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.以AQ、PQ为边作平行四边形AQPD,连接DQ,交AB于点E.设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
,AC=8cm,BC=6cm.点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.以AQ、PQ为边作平行四边形AQPD,连接DQ,交AB于点E.设运动的时间为t(单位:s)(0≤t≤4).解答下列问题: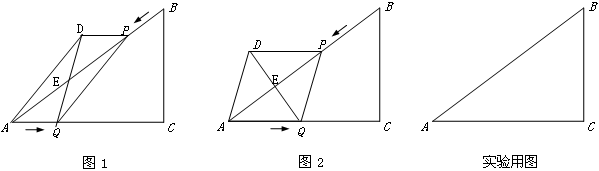
(1)用含有t的代数式表示AE=_____________;
(2)当t为何值时,DQ=AP;
(3)如图2,当t为何值时,平行四边形AQPD为菱形;
(4)直接写出:当DQ的长最小时,t的值.
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC交AC的延长线于点E,OE交AD于点F。
(1)求证:DE是⊙O的切线;
(2)若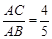 ,求
,求 的值;
的值;
(3)在(2)的条件下,若⊙O直径为10,求△EFD的面积.
某电脑经销商计划同时购进一批电脑机箱和液晶显示器,若购进电脑机箱10台和液晶显示器8台,共需要资金7000元;若购进电脑机箱2台和液晶显示器5台,共需要资金4120元.
(1)每台电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商计划购进这两种商品共50台,而可用于购买这两种商品的资金不超过22240元.根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元.该经销商希望销售完这两种商品,所获利润不少于4100元.试问:该经销商有哪几种进货方案?哪种方案获利最大?最大利润是多少?
关于x的方程kx2+(k+2)x+ =0有两个不相等的实数根.
=0有两个不相等的实数根.
(1)求k的取值范围;
(2)当k=4时方程的两根分别为x1 、x2,直接写出x1 +x2 ,x1 x2的值;
(3)是否存在实数k使方程的两个实数根的倒数和等于0?若存在,求出k的值,若不存在,说明理由。