大润发超市进了一批成本为8元/个的文具盒。调查发现: 这种文具盒每个星期的销售量
个）与它的定价
（元/个）的关系如图所示：
（1）求这种文具盒每个星期的销售量个）与它的定价（元/个）之间的函数关系式（不必写出自变量的取值范围）
（2）每个文具盒定价是多少元时，超市每星期销售这种文具盒（不考虑其他因素）可获得的利润最高？最高利润是多少?
（本小题9分）某水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克．
（1）现该商场要保证每天盈利6000元，同时又要顾客得到实惠，那么每千克应涨价多少元？
（2）若该商场单纯从经济角度看，每千克这种水果涨价多少元，能使商场获利最多？
（本小题8分）已知：如图，C，D是以线段AB为直径的⊙O上的两点，且四边形OBCD是菱形．求证：
．
（本小题8分）已知抛物线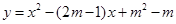
．
（1）求证：此抛物线与x轴必有两个不同的交点；
（2）若此抛物线与直线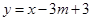
的一个交点在y轴上，求m的值．
如图，利用一面墙（墙的长度为20m），用34m长的篱笆围成两个鸡场，中间用一道篱笆隔开，每个鸡场均留一道1m宽的门，设AB的长为x米。
（1）若两个鸡场总面积为96m2，求x；
（2）若两个鸡场的面积和为S，求S关于x的关系式；
（3）两个鸡场面积和S有最大值吗？若有，最大值是多少？
如图，抛物线
与x轴交于A，B两点，与直线
相交于B，C两点，连结A，C两点。 
（1）写出直线BC的解析式
（2）求△ABC的面积