已知定义域为 的二次函数的最小值为0,且有
的二次函数的最小值为0,且有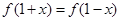 ,直线
,直线 的图象与
的图象与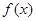 的图象交于两点,两点间的距离为
的图象交于两点,两点间的距离为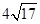 ,数列
,数列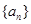 满足
满足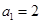
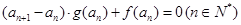 .
.
(1)求函数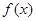 的解析式;
的解析式;
(2)求证数列 是等比数列;
是等比数列;
(3)设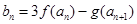 ,求数列{
,求数列{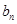 }的最小值及相应的
}的最小值及相应的
(本小题满分16分)设命题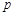 :方程
:方程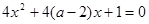 无实数根; 命题
无实数根; 命题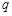 :函数
:函数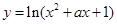 的值域是
的值域是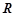 .如果命题
.如果命题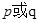 为真命题,
为真命题,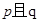 为假命题,求实数
为假命题,求实数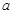 的取值范围.
的取值范围.
(本小题满分16分)
若曲线C: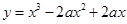 上任意点处的切线的倾斜角都为锐角,且a为整数。
上任意点处的切线的倾斜角都为锐角,且a为整数。
(1)求曲线C的解析式;
(2)求过点(1,1)的曲线的切线方程。
(本小题满分15分)已知函数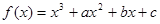 ,曲线
,曲线 在点
在点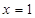 处的切线为
处的切线为 若
若 时,
时, 有极值.
有极值.
(1)求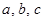 的值;
的值;
(2)求 在
在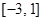 上的最大值和最小值.
上的最大值和最小值.
(本小题满分12分)命题甲:“方程x2+mx+1=0有两个相异负根”,命题乙:“方程4x2+4(m-2)x+1=0无实根”,这两个命题有且只有一个成立,试求实数m的取值范围。
已知 是函数
是函数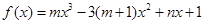 的一个极值点,其中
的一个极值点,其中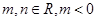 ,
,
(1)求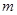 与
与 的关系式;
的关系式;
(2)求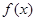 的单调区间;
的单调区间;
(3)当 时,函数
时,函数 的图象上任意一点的切线斜率恒大于
的图象上任意一点的切线斜率恒大于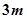 ,求
,求 的取值范围.
的取值范围.