如图所示，两块平行金属极板MN水平放置，板长L＝1 m．间距d＝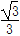
m，两金属板间电压UMN＝1×104 V；在平行金属板右侧依次存在ABC和FGH两个全等的正三角形区域，正三角形ABC内存在垂直纸面向里的匀强磁场B1，三角形的上顶点A与上金属板M平齐，BC边与金属板平行，AB边的中点P恰好在下金属板N的右端点；正三角形FGH内存在垂直纸面向外的匀强磁场B2.已知A、F、G处于同一直线上，B、C、H也处于同一直线上．AF两点的距离为
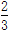m．现从平行金属板MN左端沿中心轴线方向入射一个重力不计的带电粒子，粒子质量m＝3×10－10 kg，带电荷量q＝＋1×10－4 C，初速度v0＝1×105 m/s.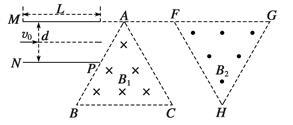
(1)求带电粒子从电场中射出时的速度v的大小和方向；
(2)若带电粒子进入中间三角形区域后垂直打在AC边上，求该区域的磁感应强度B1；
(3)若要使带电粒子由FH边界进入FGH区域并能再次回到FH界面，求B2应满足的条件．
我国月球探测计划“嫦娥工程”已经启动，科学家对月球的探索会越来越深入。
（1）若已知地球半径为R，地球表面的重力加速度为g，月球绕地球运动的周期为T，月球绕地球的运动近似看做匀速圆周运动，试求出月球绕地球运动的轨道半径；
（2）若宇航员随登月飞船登陆月球后，在月球表面高度为h的某处以速度v0水平抛出一个小球，小球飞出的水平距离为x。已知月球半径为R月，引力常量为G，试求出月球的质量M月。
“折返跑”是耐力跑的替代项目。这个项目既能发展学生的速度和灵敏素质，又能提高变换方向的能力，是一项很有价值的锻炼项目。在某次“20米折返跑”测试中，受试者在平直跑道上听到“跑”的口令后，在起点终点线前全力跑向正前方20米处的折返线，测试员同时开始计时。受试者到达折返线时，用手触摸折返线处的物体（如木箱），再转身跑向起点终点线，当胸部到达起点终点线的垂直面时，测试员停表，所计时间即为“折返跑”的成绩，如图所示。设受试者起跑的加速度为4.0 m/s2，运动过程中的最大速度为6.4 m/s，到达折返线处时需减速到零，加速度的大小为8.0 m/s2，返回时达到最大速度后不需减速，保持最大速度冲线。受试者在加速和减速阶段的运动均可视为匀变速直线运动。求该受试者“折返跑”的成绩为多少秒？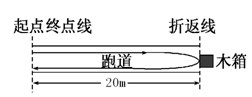
如图所示，平行金属导轨竖直放置，导轨间距离为L，仅在虚线MN以下的空间存在着匀强磁场，磁感应强度大小为B，磁场方向垂直导轨面向里，导轨上端跨接一定值电阻R，质量为m的金属棒两端各套在导轨上并可在导轨上无摩擦滑动，导轨和金属棒的电阻不计，将金属棒从导轨O处由静止释放，刚进入磁场时速度为v，到达磁场中P处时金属棒开始做匀速直线运动，O点和P点到MN的距离相等，求：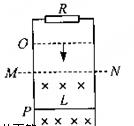
（1）求金属棒刚进入在磁场时所受安培力F1的大小；
（2）求金属棒运动到P处的过程中，电阻上共产生多少热量？
一粗细均匀的U型玻璃管竖直放置，短臂端封闭，长臂端（足够长）开口向上，短臂内封有一定质量的理想气体。初始状态时管内各段长度如图所示，密闭气体的温度为27℃。大气压强为75cmHg，求：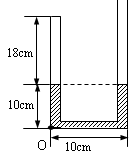
（1）若沿长臂的管壁缓慢加入5cm的水银柱并与下方的水银合为一体，为使密闭气体保持原来的长度，应使气体的温度变为多少？
（2）在第（1）小题的情况下，要使两端玻璃管中水银面相平，则气体的温度变为多少？
发电机的输出电压是220V，输出的电功率是44kW，输电线的总电阻是0.2Ω.求：
（1）若直接供电，用户得到的电功率是多少？
（2）若变电站用匝数比是1∶10的升压理想变压器，经相同的输电线后，再用匝数比是10∶1的理想变压器降压后供给用户，则用户得到的电功率又是多少？