已知数列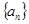 的前
的前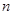 项和
项和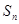 与通项
与通项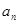 满足
满足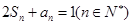 .
.
(1)求数列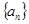 的通项公式;
的通项公式;
(2)数列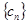 满足
满足 ,求证:
,求证: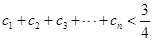 .
.
.(本小题满分12分)
在△ABC中,角A、B、C的对应边分别为a,b,c,且满足a2-ab+b2=c2.
(1)求角C;
(2)若△ABC的面积为,c=2,求a+b的值.
:已知矩阵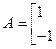
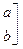 ,A的一个特征值
,A的一个特征值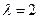 ,其对应的特征向量是
,其对应的特征向量是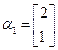 .
.
(Ⅰ)求矩阵 ;
;
(Ⅱ)求直线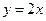 在矩阵M所对应的线性变换下的像的方程
在矩阵M所对应的线性变换下的像的方程
:已知函数 (a为常数)是R上的奇函数,函数
(a为常数)是R上的奇函数,函数 是区间[-1,1]上的减函数.
是区间[-1,1]上的减函数.
(I)求a的值;
(II)若 上恒成立,求t的取值范围;
上恒成立,求t的取值范围;
(III)讨论关于x的方程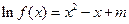 解的情况,并求出相应的m的取值范围.
解的情况,并求出相应的m的取值范围.
:已知椭圆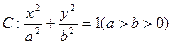 经过点
经过点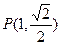 ,且两焦点与短轴的一个端点构成等腰直角三角形。
,且两焦点与短轴的一个端点构成等腰直角三角形。
(1)求椭圆的方程;
(2)动直线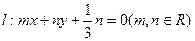 交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T。若存在,求出点T的坐标;若不存在,请说明理由。
交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T。若存在,求出点T的坐标;若不存在,请说明理由。
: 如图,ABCD是块矩形硬纸板,其中AB=2AD= 2
如图,ABCD是块矩形硬纸板,其中AB=2AD= 2 ,E为DC中点,将它沿AE折成直二面角D-AE-B.
,E为DC中点,将它沿AE折成直二面角D-AE-B.
(Ⅰ)求证:AD⊥平面BDE;
(Ⅱ)求二面角B-AD-E的余弦值.