函数 的定义域为R,若
的定义域为R,若 是奇函数,
是奇函数, 是偶函数. 下列四个结论:
是偶函数. 下列四个结论:
① ②
② 的图像关于点
的图像关于点 对称
对称
③ 是奇函数④
是奇函数④ 的图像关于直线
的图像关于直线 对称
对称
其中正确命题的个数是:
| A.1 | B.2 | C.3 | D.4 |
如图,正方体 的棱长为1,线段
的棱长为1,线段 上有两个动点E、F,且
上有两个动点E、F,且 ,则下列结论中错误的是
,则下列结论中错误的是
A. 直 直 |
B. |
C.三棱锥 的体积为定值 的体积为定值 |
D.异面直线 所成的角为定值 所成的角为定值 |

椭圆 的两焦点分别是
的两焦点分别是 ,等边
,等边 的边
的边 与该椭圆分别相交于
与该椭圆分别相交于 两点,且
两点,且 ,则该椭圆的离心率为
,则该椭圆的离心率为
A. |
B. |
C. |
D. |
5名上海世博会形象大使分别到香港、澳门、台湾进行世博会宣传,每个地方至少去1名形象大使,则不同的分派方法共有
| A.280种 | B.240种 | C.180种 | D.150种 |
将函数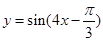 的图像上各点的横坐标伸长到原来的2倍,再向左平移
的图像上各点的横坐标伸长到原来的2倍,再向左平移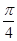 个单位,得到的函数的一条对称轴是
个单位,得到的函数的一条对称轴是
A.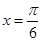 |
B.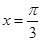 |
C.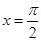 |
D.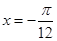 |