已知椭圆C的中心在原点,焦点y在轴上,焦距为 ,且过点M
,且过点M .
.
(1)求椭圆C的方程;
(2)若过点 的直线l交椭圆C于A、B两点,且N恰好为AB中点,能否在椭圆C上找到点D,使△ABD的面积最大?若能,求出点D的坐标;若不能,请说明理由.
的直线l交椭圆C于A、B两点,且N恰好为AB中点,能否在椭圆C上找到点D,使△ABD的面积最大?若能,求出点D的坐标;若不能,请说明理由.
(南京市2002年二模)某公司生产的A型商品通过租赁柜台进入某商场销售.第一年,商 场为吸引厂家,决定免收该年管理费,因此,该年A型商品定价为每件70元,销售量为 11.8万件.第二年,商场开始对该商品征收比率为p%的管理费(即每销售100元要征收p元),于是该商品的定价上升为每件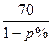 元,预计年销售量将减少p万件.
元,预计年销售量将减少p万件.
(1)将第二年商场对商品征收的管理费y(万元)表示成p的函数,并指出这个函数的定义域;
(2)要使第二年商场在此项经营中收取的管理费不少于14万元,则商场对该商品征收管理费的比率p%的范围是多少?
(3)第二年,商场在所收费不少于14万元的前提下,要让厂家获得最大销售金额,则p 应为多少?
已知直线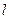 是半径为3的圆
是半径为3的圆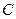 的一条切线,
的一条切线,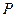 是平面上的一动点,作
是平面上的一动点,作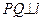 ,垂足为
,垂足为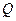 ,且
,且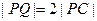 ;
;
(1)、试问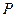 点的轨迹是什么样的曲线
点的轨迹是什么样的曲线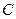 ?求出该曲线的方程;
?求出该曲线的方程;
(2)、过圆心作直线交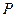 点的轨迹于
点的轨迹于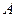 、
、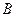 两点,若
两点,若 ,求直线
,求直线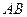 的方程。
的方程。
已知函数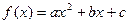
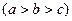 ,点
,点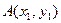 、
、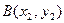 是该函数图象上的两点,且满足
是该函数图象上的两点,且满足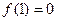 ,
, ;
;
(1)、求证: ;
;
(2)、问是否能够保证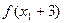 和
和 中至少有一个为正数?请证明你的结论。
中至少有一个为正数?请证明你的结论。
已知函数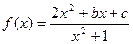
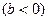 的值域为
的值域为 ;
;
(1)、求实数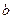 、
、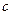 的值;
的值;
(2)、判断函数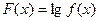 在
在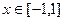 上的单调性,并给出证明;
上的单调性,并给出证明;
(3)、若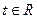 ,求证:
,求证: 。
。
对于任意的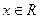 ,均有
,均有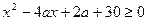 (
(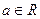 ),求关于
),求关于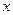 的方程
的方程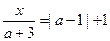 的根的范围。
的根的范围。