已知圆
.
（1）若直线
过点
，且与圆
相切，求直线的方程；
（2）若圆
的半径为4，圆心在直线
：
上，且与圆内切，求圆 的方程．
已知函数f(x)=
x3-x,数列{an}满足条件:a1≥1,an+1≥f'(an+1).试比较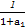
+
+
+…+
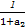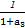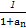与1的大小,并说明理由.
设函数f(x)满足2f(x)-f(
)=4x-
+1,数列{an}和{bn}满足下列条件:a1=1,an+1-2an=f(n),bn=an+1-an(n∈N*).
(1)求f(x)的解析式.
(2)求{bn}的通项公式bn.
(3)试比较2an与bn的大小,并证明你的结论.
用数学归纳法证明不等式:
+
+…+
>
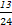(n∈N*且n>1).
用数学归纳法证明: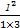
+
+…+
=
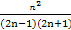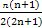(n∈N*).
已知函数f(x)=
在点(-1,f(-1))处的切线方程为x+y+3=0.
(1)求函数f(x)的解析式.
(2)设g(x)=lnx.求证:g(x)≥f(x)在[1,+∞)上恒成立.