椭圆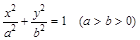
的离心率是
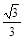，它被直线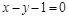
截得的弦长是
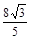，求椭圆的方程．
20．（本小题满分12分）
已知数列{an}的前n项和Sn=3―an―
，
．
（I）求证：
是等差数列；
（II）求an的最大值．
19．（本小题满分12分）
有甲、乙两箱产品，甲箱共装8件，其中一等品5件，二等品3件；乙箱共装4件，其中一等品3件，二等品1件．现采用分层抽样方法（层内采用不放回简单随机抽样）从甲、乙两箱中共抽取产品3件．
（Ⅰ）求从甲、乙两箱中各抽取产品的件数；
（Ⅱ）求抽取的3件产品中至少有2件是一等品的概率．
18．（本小题满分12分）
如图，在四棱锥V－ABCD中，底面ABCD是边长为2
的菱形，∠BAD=60°，侧面VAD⊥底面ABCD，VA=VD，E为AD的中点．
（Ⅰ）求证：平面VBE⊥平面VBC；
（Ⅱ）当直线VB与平面ABCD所成的角为30°时，求面VBE与平面VCD所成锐二面角的大小．
 |
17．（本小题满分10分）
已知△ABC的三个内角A、B、C满足sinC=
（1―cosC）=2sin2A+sin（A―B）．
求A的大小．
已知圆C1的方程为
动圆C与圆C1、C2相外切。
（I）求动圆C圆心轨迹E的方程；
（II）若直线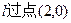
且与轨迹E交于P、Q两点。
①设点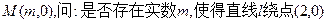
无论怎样转动，都有
成立？若存在，求出实数m的值；若不存在，请说明理由；
②过P、Q作直线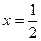
的垂线PA、QB，垂足分别为A、B，记
的取值范围。