设数列 的前
的前 项和为
项和为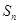 ,已知
,已知 ,且
,且
 .
.
(Ⅰ)证明: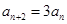 ;
;
(Ⅱ)求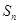 .
.
在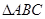 中,
中,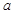 ,
,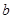 ,
,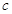 分别是三内角A,B,C所对的三边,已知
分别是三内角A,B,C所对的三边,已知 .
.
(1)求角A的大小;
(2)若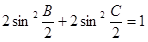 ,试判断
,试判断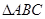 的形状.
的形状.
已知 ,且0<
,且0< <
< <
< .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 .
.
已知函数 (
( ,
, 是不同时为零的常数).
是不同时为零的常数).
(1)当 时,若不等式
时,若不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(2)求证:函数 在
在 内至少存在一个零点.
内至少存在一个零点.
已知函数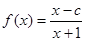 ,其中
,其中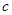 为常数,且函数
为常数,且函数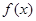 图像过原点.
图像过原点.
(1)求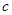 的值;
的值;
(2)证明:函数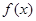 在[0,2]上是单调递增函数;
在[0,2]上是单调递增函数;
(3)已知函数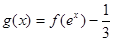 ,求g(x)≥0时x的取值范围.
,求g(x)≥0时x的取值范围.
A、B、C、D、E五位学生的数学成绩x与物理成绩y(单位:分)如下表:
 |
80 |
75 |
70 |
65 |
60 |
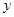 |
70 |
66 |
68 |
64 |
62 |
(1)请根据上表提供的数据,用最小二乘法求出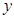 关于
关于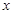 的线性回归方程
的线性回归方程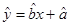 ;
;
(参考数值: 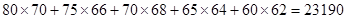 ,
,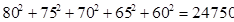 )
)
(2)若学生F的数学成绩为90分,试根据(1)求出的线性回归方程,预测其物理成绩(结果保留整数).