已知等差数列{an}的公差不为零,a1=25,且 ,
,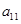 ,
,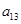 成等比数列.
成等比数列.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)求 +a4+a7+…+a3n-2.
+a4+a7+…+a3n-2.
(本小题12分)
已知 均为正数,证明:
均为正数,证明: 并确定为
并确定为 何值时,等号成立。
何值时,等号成立。
(本小题12分)
设函数 。
。
(1)若曲线 在点
在点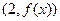 处与直线
处与直线 相切,求
相切,求 的值;
的值;
(2)求函数 的单调区间与极值点。
的单调区间与极值点。
(本小题10分)
已知 且
且 求
求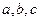 的值
的值
(本小题满分12分)
已 知椭圆
知椭圆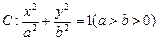 的离心率为
的离心率为 其左、右焦
其左、右焦 点分别为
点分别为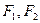 ,点P是坐标平面内一点,且
,点P是坐标平面内一点,且 (O为坐标原点)。
(O为坐标原点)。
(1)求椭圆C的方程;
(2) 过点
过点 且斜率为k的动直线
且斜率为k的动直线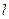 交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出M的坐标;若不存在,说明理由。
交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出M的坐标;若不存在,说明理由。
(本小题满分12分)
已知双曲线过点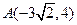 ,它的渐进线方程为
,它的渐进线方程为
(1)求双曲线的标准方程。
(2)设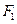 和
和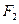 分别是双曲线的左、右焦点,点
分别是双曲线的左、右焦点,点 在双曲线上,且
在双曲线上,且
求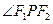 的大小。
的大小。