如图,四棱锥 中,底面
中,底面 为矩形,
为矩形,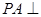 平面
平面 ,
,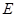 是
是 的中点.
的中点.
(1)证明: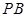 //平面
//平面 ;
;
(2)设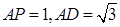 ,三棱锥
,三棱锥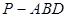 的体积
的体积 ,求
,求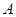 到平面
到平面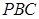 的距离.
的距离.
已知 .
.
(I)求函数 的定义域;
的定义域;
(II) 判断函数 的奇偶性;
的奇偶性;
(III)求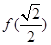 的值.
的值.
已知向量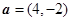 ,
, .
.
(I) 若 ,
,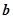 共线,求
共线,求 的值;
的值;
(II)若
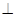
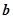 ,求
,求 的值;
的值;
(III)当 时,求
时,求 与
与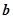 夹角
夹角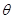 的余弦值.
的余弦值.
已知椭圆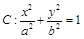
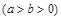 的离心率为
的离心率为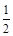 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线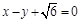 相切.
相切.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设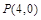 ,
,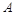 ,
, 是椭圆
是椭圆 上关于
上关于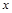 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆 于另一点
于另一点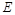 ,证明直线
,证明直线 与
与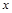 轴相交于定点
轴相交于定点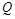 ;
;
(Ⅲ)在(Ⅱ)的条件下,过点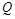 的直线与椭圆
的直线与椭圆 交于
交于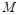 ,
, 两点,求
两点,求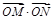 的取值范围.
的取值范围.
已知数列{an}满足an+1=
(Ⅰ)若方程f(x)=x的解称为函数y=f(x)的不动点,求an+1=f(an)的不动点的值;
(Ⅱ)若a1=2,bn= ,求证:数列{lnbn}是等比数列,并求数列{bn}的通项.
,求证:数列{lnbn}是等比数列,并求数列{bn}的通项.
(Ⅲ)当任意nÎN*时,求证:b1+b2+b3+…+bn<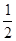
设二次函数f(x)=mx2+nx+t的图像过原点,g(x)=ax3+bx−3(x>0),f(x), g(x)的导函数为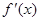 ,g¢(x),且
,g¢(x),且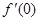 ="0,"
="0,"  =−2,f(1)="g(1),"
=−2,f(1)="g(1)," 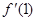 =g¢(1).
=g¢(1).
(Ⅰ)求函数f(x),g(x)的解析式;
(Ⅱ)求F(x)=f(x)−g(x)的极小值;
(Ⅲ)是否存在实常数k和m,使得f(x)³kx+m和g(x)£kx+m成立?若存在,求出k和m的值;若不存在,说明理由.