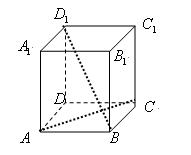
如图所示,在多面体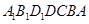 ,四边形
,四边形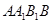 ,
, 均为正方形,
均为正方形,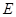 为
为 的中点,过
的中点,过 的平面交
的平面交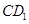 于F.
于F.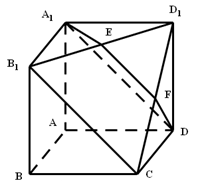
(Ⅰ)证明: ;
;
(Ⅱ)求二面角 余弦值.
余弦值.
(本小题满分12分)
如图,在四棱锥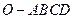 中,底面
中,底面 四边长为1的
四边长为1的
菱形,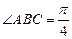 ,
,  ,
, 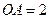 ,
, 为
为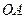 的中点.
的中点.
(Ⅰ)求异面直线AB与MD所成角的大小 ;
;
(Ⅱ)求点B到平面OCD的距离.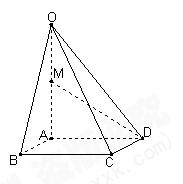
(本小题满分12分)在立体图形P-ABCD中,底面ABCD是正方形,直线PA垂直于底面,且PA=AD,E、F分别是AB、PC的中点. 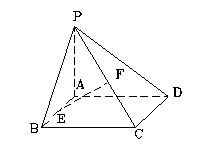 (1)求证:
(1)求证: 平面PAD;
平面PAD;
(2)求证:直线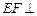 平面PCD.
平面PCD.
(本小题满分13分)
已知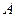 是边长为
是边长为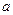 的正三角形
的正三角形 所在平面外一点,
所在平面外一点,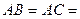
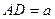 ,
,
点 、
、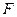 分别是
分别是 、
、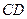 中点,
中点,
(1)求证:  为异面直线
为异面直线 与
与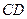 的公垂线段
的公垂线段
(2)求异面直线 与
与 的距离.
的距离.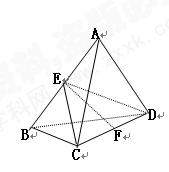
(本小题满分13分)
平面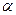 内有一个正六边形ABCDEF,它的中心是O,边长是2cm.OS⊥
内有一个正六边形ABCDEF,它的中心是O,边长是2cm.OS⊥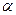 ,OS=4cm.
,OS=4cm.
求:点S到这个正六边形顶 点和边的距离.
点和边的距离.
(本小题满分13分)在正方体ABCD-A1B1C1D1中,
(1)找出平面AC的斜线BD1在平面AC内的射影;
(2)直线BD1和直线AC的位置关系如何?
(3)直线BD1和直线AC所成的角是多少度?