设函数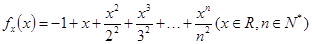 ,证明:
,证明:
(Ⅰ)对每个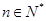 ,存在唯一的
,存在唯一的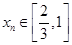 ,满足
,满足 ;
;
(Ⅱ)对任意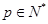 ,由(Ⅰ)中
,由(Ⅰ)中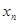 构成的数列
构成的数列 满足
满足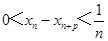 .
.
如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(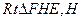 是直角
是直角 顶点)来处理污水,管道越长,污水净化效果越好。设计要求管道的接口H是AB的中点,E、F分别落在线段BC、AD上,已知AB=20米,
顶点)来处理污水,管道越长,污水净化效果越好。设计要求管道的接口H是AB的中点,E、F分别落在线段BC、AD上,已知AB=20米,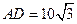 米,记
米,记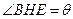 。
。
(1)试将污水净化管道的长度L表示为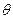 的函数,并写出定义域;
的函数,并写出定义域;
(2)若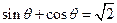 ,求此时管道的长度L;
,求此时管道的长度L;
(3)问:当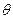 取何值时,污水净化效果最好?并求出此时管道的长度。
取何值时,污水净化效果最好?并求出此时管道的长度。
.已知数列 是等比数列,
是等比数列, 是等差数列,且
是等差数列,且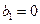 ,数列
,数列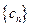 满足
满足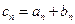 ,其前四项依次为1,
,其前四项依次为1,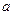 ,
,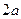 ,2,求数列
,2,求数列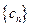 的前n项和
的前n项和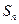 。
。
已知函数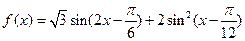 。
。
①求函数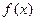 的最小正周期和单调递增区间
的最小正周期和单调递增区间 ;
;
②若 ,求函数
,求函数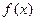 的最大值及取最大值时对应的
的最大值及取最大值时对应的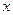 值。
值。
(本小题满分12分)
已知抛物线 (
( )的焦点为椭圆
)的焦点为椭圆 的右焦点,点
的右焦点,点 、
、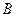 为抛物线上的两点,
为抛物线上的两点,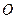 是抛物线的顶点,
是抛物线的顶点,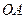 ⊥
⊥ .
.
(Ⅰ)求抛物线的标准方程;
(Ⅱ)求证:直线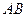 过定点
过定点 ;
;
(Ⅲ)设弦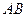 的中点为
的中点为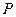 ,求点
,求点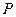 到直线
到直线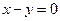 的距离的最小值.
的距离的最小值.
(本小题满分12分) 已知函数
已知函数 ,设
,设 ,
,
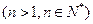 .
. (Ⅰ)求
(Ⅰ)求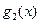 ,
, 的表达式,并直接写出
的表达式,并直接写出 的表达式;
的表达式;
(Ⅱ)设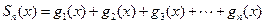 ,
,
若关于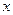 的函数
的函数
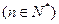 在区间
在区间 上的最小值为
上的最小值为 ,求
,求 的值.
的值.