已知函数f(x)=ex+ax2-ex,a∈R.
(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线平行于x轴,求函数f(x)的单调区间;
(Ⅱ)试确定a的取值范围,使得曲线y=f(x)上存在唯一的点P,曲线在该点处的切线与曲线只有一个公共点P.
(本题满分12分)
已知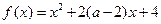 ,
,
(1)如果对一切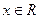 ,
,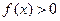 恒成立,求实数
恒成立,求实数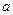 的取值范围;
的取值范围;
(2)如果对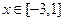 ,
,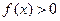 恒成立,求实数
恒成立,求实数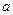 的取值范围.
的取值范围.
(本小题满分12分)
三棱柱ABC—A1B1C1中,CC1⊥平面ABC,△ABC是边长为2的等边三角形,D为AB边中点,且CC1="2AB."
(1)求证:平面C1CD⊥平面ABC;
(2)求证:AC1∥平面CDB1;
(3)求三棱锥D—CBB1的体积.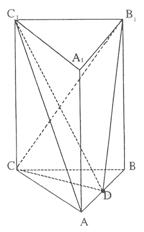
(本题满分12分)
如图,圆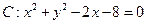 内有一点
内有一点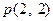 ,过点
,过点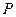 作直线
作直线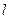 交圆
交圆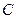 于
于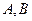 两点.
两点.
(1)当弦AB最长时,求直线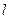 的方程;
的方程;
(2)当直线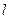 被圆
被圆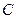 截得的弦长为
截得的弦长为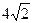 时,求
时,求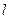 的方程.
的方程.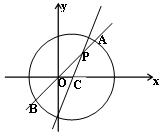
已知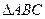 中,
中,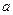 、
、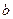 、
、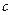 是三个内角
是三个内角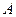 、
、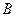 、
、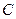 的对边,关于
的对边,关于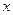 的不等式
的不等式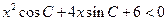 的解集是空集.
的解集是空集.
(1)求角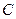 的最大值;
的最大值;
(2)若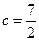 ,
,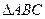 的面积
的面积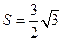 ,求当角
,求当角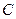 取最大值时
取最大值时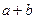 的值.
的值.
如图,设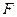 是椭圆
是椭圆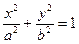 (a>b>0)的左焦点,直线
(a>b>0)的左焦点,直线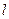 为对应的准线,直线
为对应的准线,直线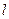 与
与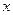 轴交于
轴交于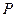 点,
点, 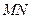 为椭圆的长轴,已知
为椭圆的长轴,已知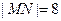 ,且
,且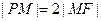 .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)求证:对于任意的割线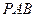 ,恒有
,恒有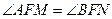 ;
;
(Ⅲ)求△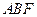 面积的最大值.
面积的最大值.