随机观测生产某种零件的某工厂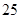
名工人的日加工零件数（单位：件），获得数据如下：
、
、
、
、
、
、
、、、
、
、
、
、、
、
、
、、
、、
、、
、
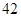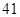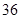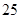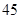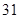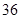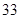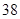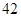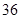、，根据上述数据得到样本的频率分布表如下：
| 分组 |
频数 |
频率 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
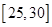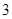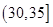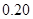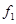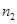（1）确定样本频率分布表中、、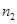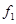和的值；
（2）根据上述频率分布表，画出样本频率分布直方图；
（3）根据样本频率分布直方图，求在该厂任取
人，至少有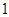
人的日加工零件数落在区间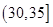的概率．
已知f(x)＝logax，g(x)＝2loga(2x＋t－2)(a>0，a≠1，t∈R)．
(1)当t＝4，x∈[1,2]，且F(x)＝g(x)－f(x)有最小值2时，求a的值；
(2)当0<a<1，x∈[1,2]时，有f(x)≥g(x)恒成立，求实数t的取值范围．
已知函数
。
（1）求
的最小正周期和单调递增区间；
（2）将按向量
平移后图像关于原点对称，求当
最小时的。
设集合A＝{x|x2－3x＋2＝0}，B＝{x|x2＋2(a＋1)x＋(a2－5)＝0}．
(1)若A∩B＝{2}，求实数a的值；
(2)若A∪B＝A，求实数a的取值范围．
画出不等式组
表示的平面区域，并求出此不等式组的整数解．
预算用
元购买单价为
元的桌子和
元的椅子，并希望桌椅的总数尽可能多，但椅子数不能少于桌子数，且不多于桌子数的
倍．问：桌、椅各买多少才合适？