某校甲、乙两个班级各有5名编号为1，2，3，4，5的学生进行投篮训练，每人投10次，投中的次数统计如下表：
| 学生 |
1号 |
2号 |
3号 |
4号 |
5号 |
| 甲班 |
6 |
5 |
7 |
9 |
8 |
| 乙班 |
4 |
8 |
9 |
7 |
7 |
（Ⅰ）从统计数据看，甲乙两个班哪个班成绩更稳定（用数据说明）？
（Ⅱ） 若把上表数据作为学生投篮命中率，规定两个班级的1号和2号两名同学分别代表自己的班级参加比赛，每人投篮一次，将甲、乙两个班两名同学投中的次数之和分别记作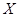
和
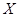，试求和的分布列和数学期望．
是平行四边形
平面外一点，
分别是
上的点，且
=
，求证：
平面
，且直线
与
都相交，求证：直线
共面。
为空间四边形
的边
上的点，且
．求证：
. 