某公司为了解用户对其产品的满意度，从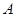
，
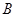两地区分别随机调查了20个用户，得到用户对产品的满意度评分如下：
（Ⅰ）根据两组数据完成两地区用户满意度评分的茎叶图，并通过茎叶图比较两地区满意度评分的平均值及分散程度（不要求计算出具体值，得出结论即可）；
（Ⅱ）根据用户满意度评分，将用户的满意度从低到高分为三个等级：
| 满意度评分 |
低于70分 |
70分到89分 |
不低于90分 |
| 满意度等级 |
不满意 |
满意 |
非常满意 |
记时间C：“A地区用户的满意度等级高于B地区用户的满意度等级”．假设两地区用户的评价结果相互独立．根据所给数据，以事件发生的频率作为相应事件发生的概率，求C的概率．
（本题小满分12分）
如图，直三棱柱
中，
，
分别是
，
的中点，
．
（1）证明：
平面
；
（2）求异面直线
和
所成角的大小；
（3）当
时，求三棱锥
的体积．
（本小题满分12分）
已知等比数列
的公比
，
且
，
，
成等差数列．数列
的前
项和为
，且
．
（1）分别求出数列和数列的通项公式；
（2）设
，若
，对于
恒成立，求实数
的最小值．
如图，四棱锥
，侧面
是边长为
的正三角形，且与底面垂直，底面
是
的菱形，
为
的中点．
（1）求证：
；
（2）求点
到平面
的距离．
（本小题满分12分）
已知函数
，
．设
时
取到最大值．
（1）求的最大值及
的值；
（2）在
中，角
，
，
所对的边分别为
，
，
，
，且
，求
的值．
（本小题满分10分）
已知函数
，
．
（1）若关于
的方程
只有一个实数解，求实数
的取值范围；
（2）若当
时，不等式
恒成立，求实数的取值范围．