正方形的边长为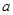
，此正方形剪去四个相同的三角形，三角形的高为
．
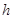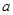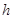（1）用和的代数式表示阴影部分的面积；
（2）若
，
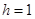，求阴影部分的面积．
某中学为筹备校庆活动，准备印制一批校庆纪念册。该纪念册每册需要10张8K大小的纸，其中4张为彩页，6张为黑白页。印制该纪念册的总费用由制版费和印刷费两部分组成，制版费与印数无关，价格为：彩页300元/张，黑白页50元/张；印刷费与印数的关系见下表。
| 印数a (单位：千册) |
1≤a＜5 |
5≤a＜10 |
| 彩色 (单位：元/张) |
2．2 |
2．0 |
| 黑白（单位：元/张） |
0．7 |
0．6 |
①印制这批纪念册的制版费为元；
②如果印制2千册，则共需费用元；
③如果该校希望印数至少为4千册，总费用至多为60000元，求印数的取值范围。（精确到0.01千册）
解分式方程：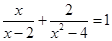
先化简，再选择一个你喜欢的整数代入求值，
，其中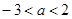
计算或化简：
(1) 
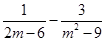．（2）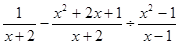
解不等式组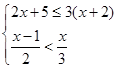
，并写出它的整数解．