如图,长为10cm,宽为6cm的长方形,在4个角剪去4个边长为x的小正方形,按折痕做一个有底无盖的长方形盒子,试求盒子的体积.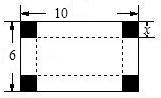
一个二次三项式x2+2x+3,将它与一个二次项ax+b相乘,积中不出现一次项,且二次项系数为1,求a,b的值?
已知6x2﹣7xy﹣3y2+14x+y+a=(2x﹣3y+b)(3x+y+c),试确定a、b、c的值.
解方程:(2x+5)(x﹣1)=2(x+4)(x﹣3), .
甲乙两人共同计算一道整式乘法:(2x+a)(3x+b),由于甲抄错了第一个多项式中a的符号,得到的结果为6x2+11x﹣10;由于乙漏抄了第二个多项中的x的系数,得到的结果为2x2﹣9x+10.请你计算出a、b的值各是多少,并写出这道整式乘法的正确结果.