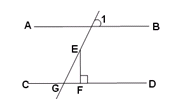
如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动。它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负。如果从A到B记为:A→B(+1,+3);从C到D记为:C→D(+1,-2)。其中第一个数表示左右方向,第二个数表示上下方向,那么图中
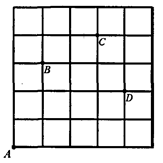
(1)A→C( , ),C→(-2, );
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(3)假如这只甲虫从A处去甲虫P处的行走路线依次为
(+2,+2),(+1,-1),(-2,+3),请在图中标出P的位置.
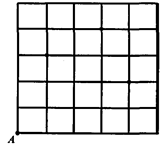
如图, 在平面直角坐标系 中, 点
中, 点 (0,8), 点
(0,8), 点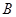 (6 , 8 ).
(6 , 8 ).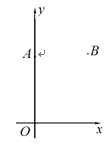
(1)只用直尺(没有刻度)和圆规, 求作一个点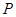 ,使点
,使点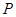 同时满足下列两个条件:(要求保留作图痕迹, 不必写出作法):
同时满足下列两个条件:(要求保留作图痕迹, 不必写出作法):
①点P到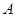 、
、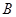 两点的距离相等;②点P到
两点的距离相等;②点P到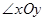 的两边的距离相等.
的两边的距离相等.
(2) 在(1)作出点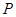 后, 在图上写出点
后, 在图上写出点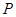 的坐标.
的坐标.
在△ABC中,∠C=90°,AC=BC=2,将一块三角板的直角顶点放在斜边AB的中点P处,将此三角板绕点P旋转,三角板的两直角边分别交射线AC、CB与点D、点E,图①,②,③是旋转得到的三种图形。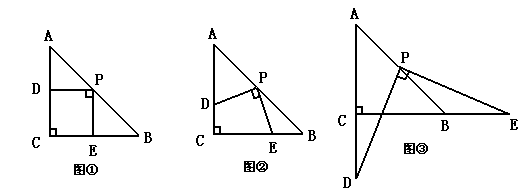
(1)观察线段PD和PE之间的有怎样的大小关系,并以图②为例,加以说明;
(2)△PBE是否构成等腰三角形?若能,指出所有的情况(即求出△PBE为等腰三角形时CE的长,直接写出结果);若不能请说明理由。
如图,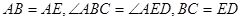 ,点
,点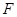 是
是 的中点
的中点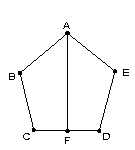
(1)请说明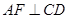 的理由
的理由
(2)连结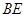 后,还能得出什么新的结论?请写出三个(不要求说明理由)
后,还能得出什么新的结论?请写出三个(不要求说明理由)
已知:如图,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N。请说明理由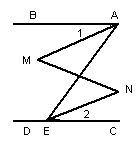
如图,直线AB∥CD,EF⊥CD于F,如果∠GEF=20°,求∠1的度数。