已知关于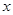 的一元二次方程
的一元二次方程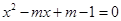 的两个实数根
的两个实数根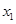 、
、 的值分别是□ABCD的两边AB、AD的长.
的值分别是□ABCD的两边AB、AD的长.
(1)如果 ,试求□ABCD的周长;
,试求□ABCD的周长;
(2)当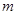 为何值时,□ABCD是菱形?
为何值时,□ABCD是菱形?
计算
(-9)-(-7)+(-6)-(+4)-(-5)
某农户承包荒山若干亩,投资7800元改造后,种果树2000棵。今年水果总产量预测为18000千克,此水果在市场上每千克售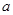 元,在果园每千克售
元,在果园每千克售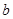 元(
元(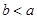 )。该农户将水果拉到市场出售平均每天出售1000千克,需8人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元。
)。该农户将水果拉到市场出售平均每天出售1000千克,需8人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元。
(1)分别用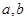 表示两种方式出售水果的收入?
表示两种方式出售水果的收入?
(2)若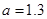 元,
元, 元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好?
元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好?
(3)该农户加强果园管理,力争到明年纯收入达到15000元,而且该农户采用了(2)中较好的出售方式出售,那么纯收入增长率是多少(纯收入=总收入-总支出)?
“十·一”黄金周期间,武汉动物园在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
| 日期 |
10月1日 |
10月2日 |
10月3日 |
10月4日 |
10月5日 |
10月6日 |
10月7日 |
| 人数变化单位:万人 |
+1.6 |
+0.8 |
+0.4 |
-0.4 |
-0.8 |
+0.2 |
-1.2 |
(1)若9月30日的游客人数记为 ,请用
,请用 的代数式表示10月2日的游客人数?
的代数式表示10月2日的游客人数?
(2)请判断七天内游客人数最多的是哪天?请说明理由。
(3)若9月30日的游客人数为2万人,门票每人10元。问黄金周期间武汉动物园门票收入是多少元?
已知:有理数m所表示的点与-1表示的点距离4个单位, 互为相反数, 且都不为零,
互为相反数, 且都不为零, 互为倒数。求:
互为倒数。求: 的值
的值
已知 ,且
,且 ,求
,求 的值
的值