某公园有一个抛物线形状的观景拱桥ABC,其横截面如图所示,在图中建立的直角坐标系中,抛物线的解析式为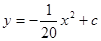 且过顶点C(0,5)(长度单位:m)
且过顶点C(0,5)(长度单位:m)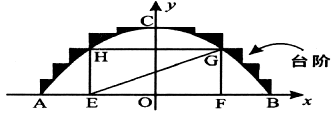
(1)直接写出c的值;
(2)现因搞庆典活动,计划沿拱桥的台阶表面铺设一条宽度为1.5 m的地毯,地毯的价格为20元/m2,求购买地毯需多少元?
(3)在拱桥加固维修时,搭建的“脚手架”为矩形EFGH(H、G分别在抛物线的左右侧上),并铺设斜面EG.已知矩形EFGH的周长为27.5m,求点G的坐标.
(本题5分)如果方程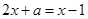 的解是
的解是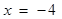 ,求
,求 的值.
的值.
解下列方程:(每题4分,共16分)
(1)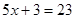
(2)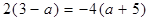
(3)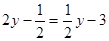
(4)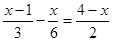
计算题:(每题4分,共16分)
(1) 12-(-18)+(-7)-15
(2)23-6×(-3)+2×(-4)
(3)
(4)
某商场销售一种西装和领带,西装每套定价500元,领带每条定价60元.“国庆节”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.方案一:买一套西装送一条领带;方案二:西装和领带都按定价的90%付款.现某客户要到该商场购买西装20套,领带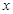 条(
条(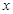 >20).
>20).
(1)若该客户按方案一购买,需付款______________元.(用含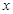 的代数式表示)若该客户按方案二购买,需付款_____________元.(用含
的代数式表示)若该客户按方案二购买,需付款_____________元.(用含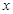 的代数式表示)
的代数式表示)
(2)若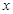 =30,通过计算说明此时按哪种方案购买较为合算?
=30,通过计算说明此时按哪种方案购买较为合算?
一只蜗牛从A点出发,在一条数轴上来回爬行,规定:向正半轴运动记为“+”,向负半轴运动记为“—”,从开始到结束爬行的各段路程(单位:cm)依次为+7,—5,—10,—8,+9,—6,+12,+4。
(1)若A点在数轴上表示的数为—2,则蜗牛停在数轴上何处,请通过计算加以说明。
(2)若蜗牛的爬行速度为每秒 ,请问蜗牛一共爬行了多少秒?
,请问蜗牛一共爬行了多少秒?