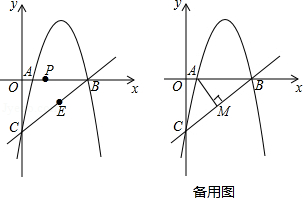
对于平面直角坐标系xOy中的点P和线段AB，给出如下定义：在-优题课

对于平面直角坐标系xOy中的点P和线段AB，给出如下定义：在线段AB外有一点P，如果在线段AB上存在两点C、D，使得∠CPD=90°，那么就把点P叫做线段AB的悬垂点．
（1）已知点A（2，0），O（0，0）
①若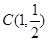，D（1，1），E（1，2），在点C，D，E中，线段AO的悬垂点是______；
②如果点P（m，n）在直线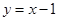上，且是线段AO的悬垂点，求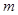的取值范围；
（2）如下图是帽形M（半圆与一条直径组成，点M是半圆的圆心），且圆M的半径是1，若帽形内部的所有点是某一条线段的悬垂点，求此线段长的取值范围．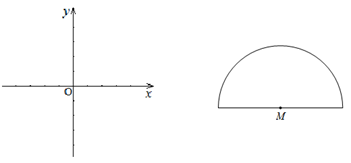

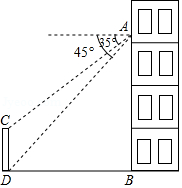
科目数学题型解答题难度中等

2019年，成都马拉松成为世界马拉松大满贯联盟的候选赛事，这大幅提升了成都市的国际影响力，如图，在一场马拉松比赛中，某人在大楼 $A$ 处，测得起点拱门 $CD$ 的顶部 $C$ 的俯角为 $35 °$ ，底部 $D$ 的俯角为 $45 °$ ，如果 $A$ 处离地面的高度 $AB = 20$ 米，求起点拱门 $CD$ 的高度．（结果精确到1米；参考数据： $\sin 35 ° \approx 0.57$ ， $\cos 35 ° \approx 0.82$ ， $\tan 35 ° \approx 0.70)$

随着科技的进步和网络资源的丰富，在线学习已经成为更多人的自主学习选择．某校计划为学生提供以下四类在线学习方式：在线阅读、在线听课、在线答题和在线讨论．为了解学生需求，该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查，并根据调查结果绘制成如下两幅不完整的统计图．

根据图中信息，解答下列问题：

（1）求本次调查的学生总人数，并补全条形统计图；

（2）求扇形统计图中“在线讨论”对应的扇形圆心角的度数；

（3）该校共有学生2100人，请你估计该校对在线阅读最感兴趣的学生人数．

先化简，再求值： $(1 - \frac{4}{x + 3}) \div \frac{x^{2} - 2 x + 1}{2 x + 6}$ ，其中 $x = \sqrt{2} + 1$ ．

（1）计算： ${(π - 2)}^{0} - 2 \cos 30 ° - \sqrt{16} + | 1 - \sqrt{3} |$ ．

（2）解不等式组： $\{\begin{matrix} 3 (x - 2) ⩽ 4 x - 5, ① \\ \frac{5 x - 2}{4} < 1 + \frac{1}{2} x \cdot ② \end{matrix}$

如图，抛物线 $y = a x^{2} + bx - 5 (a \neq 0)$ 经过 $x$ 轴上的点 $A (1, 0)$ 和点 $B$ 及 $y$ 轴上的点 $C$ ，经过 $B$ 、 $C$ 两点的直线为 $y = x + n$ ．

①求抛物线的解析式．

②点 $P$ 从 $A$ 出发，在线段 $AB$ 上以每秒1个单位的速度向 $B$ 运动，同时点 $E$ 从 $B$ 出发，在线段 $BC$ 上以每秒2个单位的速度向 $C$ 运动．当其中一个点到达终点时，另一点也停止运动．设运动时间为 $t$ 秒，求 $t$ 为何值时， $ΔPBE$ 的面积最大并求出最大值．

③过点 $A$ 作 $AM ⊥ BC$ 于点 $M$ ，过抛物线上一动点 $N$ （不与点 $B$ 、 $C$ 重合）作直线 $AM$ 的平行线交直线 $BC$ 于点 $Q$ ．若点 $A$ 、 $M$ 、 $N$ 、 $Q$ 为顶点的四边形是平行四边形，求点 $N$ 的横坐标．

试卷网试题网古诗词网作文网范文网