已知椭圆的一个顶点为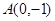 ,焦点在
,焦点在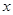 轴上,离心率为
轴上,离心率为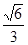 .
.
(1)求椭圆的方程;
(2)设椭圆与直线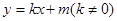 相交于不同的两点
相交于不同的两点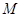 、
、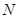 ,当
,当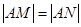 时,求
时,求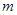 的取值范围.
的取值范围.
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为 立方米,且
立方米,且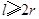 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为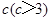 .设该容器的建造费用为
.设该容器的建造费用为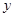 千元.
千元.
(Ⅰ)写出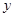 关于
关于 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(Ⅱ)求该容器的建造费用最小时的 .
.
(文)如图,从点P1(0,0)作x轴的垂线交于曲线y=ex于点Q1(0,1),曲线在Q1点处的切线与x轴交与点P2。再从P2作x轴的垂线交曲线于点Q2,依次重复上述过程得到一系列点:P1,QI;P2,Q2…Pn,Qn,记 点的坐标为(
点的坐标为( ,0)(k=1,2,…,n)。
,0)(k=1,2,…,n)。
(Ⅰ)试求 与
与 的关系(2≤k≤n);
的关系(2≤k≤n);
(Ⅱ)求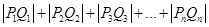
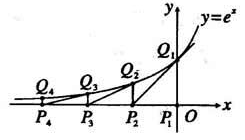
.(理)抛物线y=ax2+bx在第一象限内与直线x+y=4相切.此抛物线与x轴所围成的图形的面积记为S.求使S达到最大值的a、b值,并求Smax.
已知复数 满足,复平面内有RtΔABC,其中∠BAC=90°,点A、B、C分别对应复数
满足,复平面内有RtΔABC,其中∠BAC=90°,点A、B、C分别对应复数 ,如图所示,求z的值。
,如图所示,求z的值。
已知复数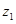 满足
满足 (
(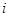 为虚数单位),复数
为虚数单位),复数 的虚部为
的虚部为 ,
,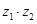 是实数,求
是实数,求 。
。