列方程解应用题:某小组计划做一批“中国结”,如果每人做5个,那么比计划多了9个;如果每人做4个,那么比计划少了15个.小组成员共有多少名?他们计划做多少个“中国结”?
如图.点A、B、C、D在⊙O上,AC⊥BD于点E,过点O作OF⊥BC于F,求证: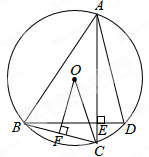
(1)△AEB∽△OFC;
(2)AD=2FO.
某旅行社为了吸引游客组团去旅游,推出了如下收费标准:
(1)若A单位组织该单位25名员工去旅游,需支付给该旅行社旅游费用_____元。
(2)若B单位共支付给该旅行社旅游费用27000元,请问B单位共有多少名员工去旅游?
已知P为等边△ABC外接圆上的一点,CP延长线和AB的延长线相交于点D,连结BP,求证: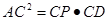
如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D。已知:AB=24cm,CD=8cm。
(1)求作此残片所在的圆(不写作法,保留作图痕迹);
(2)求(1)中所作圆的半径。
如图:小明想测量一棵树的高度AB,在阳光下,小明测得一根与地面垂直、长为1米的竹竿的影长为0.8米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),墙壁上的影长CD为1.5米,落在地面上的影长BD为3米,则树高AB为多少米.
