如图，在△ABC中，∠B=90°，AB=6米，BC=8米，动点P以2米/秒的速度从A点出发，沿AC向点C移动，同时，动点Q以1米/秒的速度从C点出发，沿CB向点B移动．当其中有一点到达终点时，它们都停止移动，设移动的时间为t秒．
（1）①当t=2．5秒时，求△CPQ的面积；
②求△CPQ的面积S（平方米）关于时间t（秒）的函数解析式；
（2）在P、Q移动的过程中，当△CPQ为等腰三角形时，直接写出t的值；
如图是由7块小立方体摆放而成的几何体，请画出它的三视图.(6分)
（本小题12分）如图，直线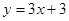
交
轴于A点，交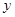
轴于B点，过A、B两点的抛物线交轴于另一点C（3,0）. 
⑴ 求抛物线的解析式;
⑵ 在抛物线的对称轴上是否存在点Q，使△ABQ是等腰三角形？若存在，求出符合条件的Q点坐标；若不存在，
请说明理由.
（本小题10分）某宾馆客房部有60个房间供游客居住，当每个房间的定价为每天200元时，
房间可以住满。当每个房间每天的定价每增加10元时，就会有一个房间空闲。对有游客入住的房间，宾馆需对每个房间每天支出20元的各种费用。
设每个房间每天的定价增加
元，求：（1）房间每天的入住量
（间）关于（元）的函数关系式；（2）该宾馆每天的房间收费
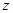（元）关于（元）的函数关系式；（3）该宾馆客房部每天的利润
（元）关于（元）的函数关系式；当每个房间的定价为每天多少元时，有最大值？最大值是多少
？
（本小题10分）已知函数y=mx2－6x＋1（m是常数）．⑴求证：不论m为何值，该函数的图象都经过y轴上的一个定点；
⑵若该函数的图象与x轴只有一个交点，求m的值．
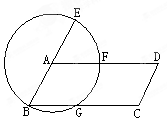
（本小题8分）如图4,平行四边形ABCD中,以A为圆心,AB为半径的圆分别交AD、BC于F、G,延长B
A交圆于E.
