如图,已知CD⊥AB于D,BE⊥AC于E,CD交BE于点O.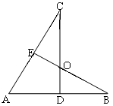
若OC=OB,求证:点O在∠BAC的平分线上
若点O在∠BAC的平分线上,求证:OC=OB
已知,如图A、F、C、D四点在一直线上,AF=CD,AB//DE,且AB=DE,求证: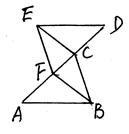
△ABC≌△DEF
∠CBF=∠FEC
如图,AD是∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,且DB=DC。求证:BE=CF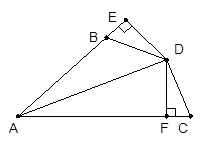
如图,(1)画出△ABC关于y轴的对称图形△A1B1C1;
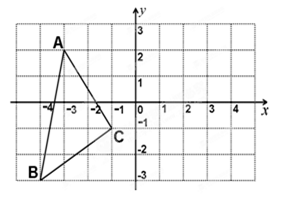
直接写出△ABC关于x轴对称的三角形△A2B2C2的各点坐标。
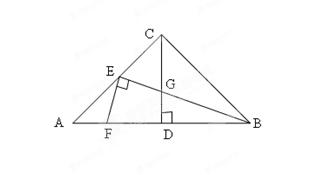
如图在△ABC 中,AC=BC, ACB=
ACB=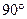 ,CD
,CD AB,垂足为D,点E在AC上,
AB,垂足为D,点E在AC上,
CE=EA, BE交CD于点G,EF BE交AB于点F,探索线段EF与EG的数量关系,
BE交AB于点F,探索线段EF与EG的数量关系,
并证明你的结论。