如图，在△ABC中，∠C=90°，AC=BC=4，D是AB的中点，点E、F分别在AC、BC边上运动（点E不与点A、C重合），且保持AE=CF，连接DE、DF、EF．在此运动变化的过程中，有下列结论：
①△DFE是等腰直角三角形；
②四边形CEDF不可能为正方形；
③四边形CEDF的面积随点E位置的改变而发生变化；
④点C到线段EF的最大距离为
．
其中正确结论的个数是（ ）
A、1个 B、2个 C、3个 D、4个
式子
在实数范围内有意义，则x的取值范围是（ ）
| A．x＜1 | B．x≥1 | C．x≤﹣1 | D．x＞1 |
已知二次函数y=ax2+bx+c的图象如图，①abc＞0；②b＜a+c；③4a+2b+c＞0；④2c＜3b；⑤a+b＞m（am+b）（m≠1），其中结论正确的有（ ）
| A．③④ | B．③⑤ | C．③④⑤ | D．②③④⑤ |
图中实线部分是半径为9m的两条等弧组成的游泳池．若每条弧所在的圆都经过另一个圆的圆心，则游泳池的周长为（ ）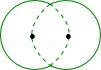
| A．12πm | B．18πm | C．20πm | D．24πm |
为解决群众看病贵的问题，有关部门决定降低药价，对某种原价为289元的药品进行连续两次降价后为256元，设平均每次降价的百分率为x，则下面所列方程正确的是（ ）
| A．289（1﹣x）2="256" | B．256（1﹣x）2=289 |
| C．289（1﹣2x）="256" | D．256（1﹣2x）=289 |
抛物线y=﹣2x2经过平移到y=﹣2x2﹣4x﹣5，平移方法是（ ）
| A．向左平移1个单位，再向上平移3各单位 |
| B．向左平移1个单位，再向下平移3个单位 |
| C．向右平移1个单位，再向上平移3个单位 |
| D．向右平移1个单位，再向下平移3个单位 |