小华同学学习了第二十五章《锐角三角比》后,对求三角形的面积方法进行了研究,得到了新的结论:如图,已知锐角△ABC,则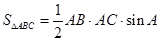

(1)试证明上述结论;
(2)运用这个新的结论,请完成下题:如图,在等腰△ABC中,AB=AC=12厘米,点P从A点出发,沿着边AB移动,点Q从C点出发沿着边CA移动,点Q的速度是1厘米/秒,点P的速度是点Q速度的2倍,若它们同时出发,设移动时间为t秒,问:当t为何值时, ?
?
如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB2=∠PCB.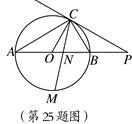
求证:PC是⊙O的切线
求证:BC=
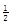 AB;
AB;点M是弧AB的中点,CM交AB于点N,若AB=4,求MN ·MC的值.
某电脑公司经销甲种型号电脑,受经济危机影响,电脑价格不断下降.今年三月份的电脑售价比去年同期每台降价1000元,如果卖出相同数量的电脑,去年销售额为10万元,今年销售额只有8万元.今年三月份甲种电脑每台售价多少元
为了增加收入,电脑公司决定再经销乙种型号电脑,已知甲种电脑每台进价为3500元,乙种电脑每台进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台,有几种进货方案?
如果乙种电脑每台售价为3800元,为打开乙种电脑的销路,公司决定每售出一台乙种电脑,返还顾客现金
 元,要使(2)中所有方案获利相同,
元,要使(2)中所有方案获利相同, 值应是多少?此时,哪种方案对公司更有利?
值应是多少?此时,哪种方案对公司更有利?
已知:如图,AB是⊙O的直径,C是⊙O上一点,CD⊥AB,垂足为点D, 是
是 的中点,
的中点, 与
与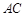 相交于点
相交于点 ,
,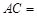 8 cm,
8 cm,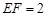 cm.
cm.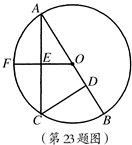
求AO的长
求
 的值.
的值.
小明和小亮是一对双胞胎,他们的爸爸买了两套不同品牌的运动服送给他们,小明和小亮都想先挑选.于是小明设计了如下游戏来决定谁先挑选.游戏规则是:在一个不透明的袋子里装有除数字以外其它均相同的4个小球,上面分别标有数字1、2、3、4.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为奇数,则小明先挑选;否则小亮先挑选用树状图或列表法求出小明先挑选的概率;
你认为这个游戏公平吗?请说明理由
某厂家新开发一种摩托车如图所示,它的大灯A射出的光线AB、AC与地面MN的夹角分别为8°和10°,大灯A与地面距离1 m.
该车大灯照亮地面的宽度BC约是多少?
一般正常人从发现危险到做出刹车动作的反应时间是0.2 s,从发现危险到摩托车完全停下所行驶的距离叫做最小安全距离,某人以60km/h的速度驾驶该车,突然遇到危险情况,立即刹车直到摩托车停止,在这过程中刹车距离是
 m,请判断该车大灯的设计是否能满足最小安全距离的要求,请说明理由.(参考数据:
m,请判断该车大灯的设计是否能满足最小安全距离的要求,请说明理由.(参考数据: ,
, ,
,  ,
,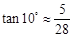 )
)