如图，是利用潮汐发电的原理图．左方为陆地和海湾，中间为水坝，其下有通道，无论涨潮或落潮，水流经过通道均可带动发电机发电．一昼夜中两次涨、落潮，四次发电．涨潮时，堵住通道，潮水涨至最高水位时打开通道，进水发电，如图甲所示；当海湾水位涨至最高时，堵住通道，如图乙所示；落潮至最低水位时，打开通道放水发电，如图丙所示．（取g=10N/kg，海水的密度1.0×103kg/m3）以下是某小型潮汐发电站的一组数据，据此回答下列问题：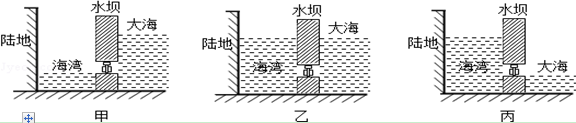
| 水坝高度 |
15m |
海湾面积 |
4.5×106m2 |
| 涨潮海湾最高水位 |
10m |
发电机日平均发电量 |
4.4×104kW•h |
| 退潮海湾最低水位 |
6m |
水轮发电机总效率 |
10% |
（1）当海湾水位涨至最高时，海湾底部所受水的压强是多少？
（2）每次涨潮（或落潮）经过通道水的质量为多少？
（3）试计算每日水流对水轮发电机做了多少功？
（4）若某次落潮过程中经过通道的水的平均流量为3.6×106m3/h，试求这次落潮过程中水流对水轮发电机做功的平均功率．
如图所示，电源电压恒定不变，若开关S1闭合，S2断开时，电流表的示数为0．6A；当S1、S2都断开时，电流表的示数为0．4A；当S1、S2都闭合时，电流表的示数为0．9A。已知R2的电阻为10Ω。求：
（1）当S1、S2都断开时，R1消耗的功率；
（2） 当S1、S2都闭合时，电路消耗的总功率。 
测出某物体的重力大小如图所示，将它浸没在水中后，测力计的示数变为0.6N，取g=10N/kg。求：物体的密度
将两个小灯泡L1：“6V，12W”和L2：“6V，6W”串联起来接在电源上，要保证两灯泡的实际电压都不超过各自的额定电压，求电源电压的最大值。
某科技小组的同学们设计了一个自动冲刷装置，该装置能把进水管供给的较小流量的
水储存到一定量后，自动开启放水阀门进行冲刷。图是该装置主要部件的截面示意图，AB是一个可以绕O点转动的轻质杠杆，OB=2OA；C是厚度为d、底面积为S的放水阀门（阀门C刚好堵住排水管管口）。将一根细绳一端系在阀门C中央，另一端系在杠杆的A点。浮筒D是一个底面积为4S的空心圆柱体，将细绳一端系在浮筒D下端中央并通过定滑轮使绳的另一端与杠杆的B点相连。当水箱中的水深为2.5h时，系在浮筒D下端的细绳刚好被拉直；当水箱中的水深为3h时，阀门C刚好被打开。在阀门C被打开前，杠杆AB始终保持水平，若细绳所受的重力以及装置的机械阻力均忽略不计，水的密度为ρ水，则放水阀C的质量是多少？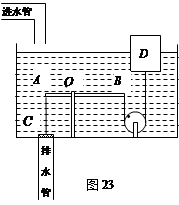 
质量为0.2kg的热水，温度从90℃降低到40℃，放出的热量是多少？
[水的比热容为4.2×103 J/（kg·℃）]