中国“史上最严交规”于2013年1月1日正式实施,其中最具争议的是闯黄灯扣分。一辆汽车正以36km/h的速度匀速行驶,在前轮距离停车线为10m处,司机发现路口的绿灯变为黄灯,该司机立即刹车。
(1)若汽车刹车时的加速度大小为5m/s2,则在刹车后3s内汽车的位移为多少?
(2)若司机的反应时间(从看到黄灯到踩下刹车的时间)为0.5s,则汽车刹车的加速度至少为多大前轮才不会压停车线。
如图所示,粒子源S可以不断地产生质量为m、电荷量为+q的粒子(重力不计).粒子从O1孔漂进(初速不计)一个水平方向的加速电场,再经小孔O2进入相互正交的匀强电场和匀强磁场区域,电场强度大小为E,磁感应强度大小为B1,方向如图.虚线PQ、MN之间存在着水平向右的匀强磁场,磁感应强度大小为B2(图中未画出).有一块折成直角的硬质塑料板abc(不带电,宽度很窄,厚度不计)放置在PQ、MN之间(截面图如图),a、c两点恰在分别位于PQ、MN上,ab=bc=L,α= 45°.现使粒子能沿图中虚线O2O3进入PQ、MN之间的区域.
(1) 求加速电压U1.
(2)假设粒子与硬质塑料板相碰后,速度大小不变,方向变化遵守光的反射定律.粒子在PQ、MN之间的区域中运动的时间和路程分别是多少?
如图所示,水平轨道上轻弹簧左端固定,弹簧处于自然状态时,其右端位于P点.现用一质量m=0.1kg的小物块 (可视为质点)将弹簧压缩后释放,物块经过P点时的速度v0=18m/s,经过水平轨道右端Q点后恰好沿光滑半圆轨道的切线进入竖直固定的圆轨道,最后物块经轨道最低点A抛出后落到B点。若物块与水平轨道间的动摩擦因数μ=0.15,R=l=1m,A到B的竖直高度h=1.25m,取g=10m/s2.
(1) 求物块到达Q点时的速度大小;
(2) 判断物块经过Q点后能否沿圆周轨道运动;
(3) 求物块水平抛出的位移大小.
如图所示在竖直平面内建立直角坐标系XOY,OY表示竖直向上的方向。已知该平面内存在沿OX轴负方向的区域足够大的匀强电场,现有一个带电量为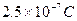 、质量为
、质量为 的小球从坐标
的小球从坐标 原点O沿Y轴正方向以某一初速度竖直向上抛出,它到达的最高点位置为图中的Q点,其坐标为(1.6,3.2),不计空气阻力,g取10m/s2。
原点O沿Y轴正方向以某一初速度竖直向上抛出,它到达的最高点位置为图中的Q点,其坐标为(1.6,3.2),不计空气阻力,g取10m/s2。
(1)指出小球带何种电荷
(2)求小球的初速度和匀强电场的场强大小
(3)求小球从O点抛出到落回X轴的过程中电势能的改变量
匀强电场中A、B、C三点构成一个直角三角形。AB=4cm,BC=3cm,把电荷量为q=-2×10-10C的点电荷从A点移到B时,电场力做功4.8×10-8 J,从B点移到电C点时,克服电场力做功4.8×10-8J,若取B点的电势为零,求A、C两点的电势和场强的大小及方向。(要求方向在图中画出)
J,从B点移到电C点时,克服电场力做功4.8×10-8J,若取B点的电势为零,求A、C两点的电势和场强的大小及方向。(要求方向在图中画出)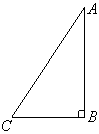
用30cm的细线将质量为m=4×10-3㎏的带电小球P悬挂在O点下,当空中有方向为水平向右,大小为E=1×104N/C的匀强电场时,小 球偏转37°后处在静止状态。
球偏转37°后处在静止状态。
(1)分析小球的带电性质
(2)求小球的带电量
(3)求细线的拉力