如图所示,边长为L的正方形PQMN区域内(含边界)有垂直纸面向外的匀强磁场,左侧有水平向右的匀强电场,场强大小为E。质量为m、电荷量为q的带正电粒子从O点由静止开始释放,O、P、Q三点在同一水平直线上,OP=L,带电粒子恰好从M点离开磁场,不计带电粒子重力,求:
(1)磁感应强度大小B;
(2)粒子从O点运动到M点经历的时间;
(3)若磁感应强度可调节(不考虑磁场变化产生的电磁感应),带电粒子从边界NM上的O′点离开磁场,O′与N点距离为 ,求磁感应强度的可能数值。
,求磁感应强度的可能数值。
(1) 下列说法中正确的有________.
| A.实验“用油膜法估测分子大小”中,油酸分子的直径等于油酸酒精溶液的体积除以相应油酸膜的面积 |
| B.布朗运动中,悬浮在液体中的固体颗粒越小、液体的温度越高,布郎运动越激烈 |
| C.分子间的距离越小,分子间引力越小,斥力越大 |
| D.液晶的光学性质与某些晶体相似,具有各向异性 |
(2) 如图所示,某种自动洗衣机进水时,洗衣机缸内水位升高,与洗衣缸相连的导热性能良好的细管中会封闭一定质量的空气,通过压力传感器感知管中的空气压力,从而控制进水量.将细管中密闭的空气视为理想气体,当洗衣缸内水位缓慢升高时,外界对空气做了0.5 J的功,则空气________(填“吸收”或“放出”)了__________的热量.(设环境温度保持不变)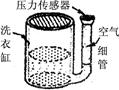
(3) 目前专家们正在研究二氧化碳的深海处理技术.实验发现,在水深300 m处,二氧化碳将变成凝胶状态.当水深超过2 500 m时,二氧化碳会浓缩成近似固体的硬胶体,可看成分子间是紧密排列的.已知二氧化碳的摩尔质量为M,阿伏加德罗常数为NA,每个二氧化碳分子的体积为V0.某状态下二氧化碳气体的密度为ρ,求该状态下体积为V的二氧化碳气体浓缩成近似固体的硬胶体后体积为多少?
在甲图中,带正电粒子从静止开始经过电势差为U的电场加速后,从G点垂直于MN进入偏转磁场。该偏转磁场是一个以直线MN为上边界、方向垂直于纸面向外的匀强磁场,磁场的磁感应强度为B,带电粒子经偏转磁场后,最终到达照相底片上的H点,如图甲所示,测得G、H间的距离为d,粒子的重力可忽略不计。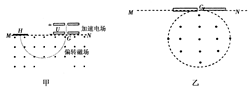
(1)设粒子的电荷量为q,质量为m。求该粒子的比荷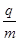 ;
;
(2)若偏转磁场的区域为圆形,且与MN相切于G点,如图乙所示,其它条件不变,要保证上述粒子从G点垂直于MN进入偏转磁场后不能打到MN边界上(MN足够长),求磁场区域的半径应满足的条件。
如图为回旋加速器的装置图,D型盒的两底边分别为a、b,且相距很近,忽略粒子在其间的运动时间,设D型盒中的匀强磁场的磁感应强度为B,D型盒的半径为R,质量为m带电量为q的正电荷在a的中点从静止释放,求: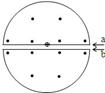
(1)带电粒子出回旋加速器时的动能
(2)从带电粒子开始运动开始计时,画出Uab一个周期内随时间t变化的图像(横轴用已知量标出)
(3)如果ab间的电压值始终保持为U,带电粒子从静止开始运动到出加速器所用的时间
带电量为Q,质量为m的原子核由静止开始经电压为U1的电场加速后进入一个平行板电容器,进入时速度和电容器中的场强方向垂直。已知:电容器的极板长为L,极板间距为d,两极板的电压为U2,重力不计,求:
(1)经过加速电场后的速度;
(2)离开电容器电场时的侧移量和偏转角的正切值。
质谱仪的工作原理图如图所示,A为粒子加速器,加速电压为U1;M为速度选择器,两板间有相互垂直的匀强磁场和匀强电场,匀强磁场的磁感应强度为B1,两板间距离为d;N为偏转分离器,内部有与纸面垂直的匀强磁场,磁感应强度为B2.一质量为m,电荷量为q的带正电的粒子由静止经加速器加速后,恰能通过速度选择器,进入分离器后做圆周运动,并打到感光板P上.不计重力,求: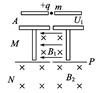
(1)粒子经粒子加速器A加速后的速度v的大小及速度选择器M两板间的电压U2.
(2)粒子在偏转分离器N的磁场中做圆周运动的半径R.
(3)某同学提出在其他条件不变的情况下,只减小加速电压U1,就可以使粒子在偏转分离器N的磁场中做圆周运动的半径减小.试分析他的说法是否正确.