同学们参照伽利略时期演示平抛运动的方法制作了如图所示的实验装置。图中水平放置的底板上竖直地固定有M板和N板。M板上部有一半径为R的
圆弧形的粗糙轨道，P为最高点，Q为最低点，Q点处的切线水平，距底板高为
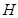。N板上固定有三个圆环。将质量为
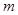的小球从P处静止释放，小球运动至Q飞出后无阻碍地通过各圆环中心，落到底板上距Q水平距离为L处。不考虑空气阻力，重力加速度为g。求：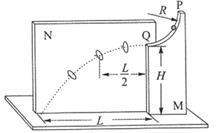
（1）距Q水平距离为
的圆环中心到底板的高度；
（2）小球运动到Q点时速度的大小以及对轨道压力的大小和方向；
（3）摩擦力对小球做的功。
如图a是研究小球在斜面上平抛运动的实验装置，每次将小球从弧型轨道同一位置静止释放，并逐渐改变斜面与水平地面之间的夹角θ，获得不同的射程x，最后作出了如图b所示的x-tanθ图象，g取l0m／s2，则：
（1）由图b可知，小球在斜面顶端水平抛出时的初速度
。实验中发现θ超过60°后，小球将不会掉落在斜面上，则斜面的长度为m。（保留1位有效数字）
（2）若最后得到的图象如图c所示，则可能的原因是（写出一个）
如图所示，在倾角为
秒的光滑斜面上有两个用轻质弹簧相连接的物块A，B，它们的质量分别为
、
，弹簧的劲度系数为
。C为一固定挡板，系统处于静止状态。现在开始用一恒力沿斜面方向拉物块A使之向上运动，若稳定后物块A、B共同以加速度
沿斜面向上匀加速运动（重力加速度为g）。求：
（1）稳定后弹簧对物块A的弹力：
（2）从恒力作用前到稳定后物块A与物块B间距离的变化量d。
如图所示，在同一竖直平面内两正对着的相向半圆光滑轨道，相隔一定的距离，虚线沿竖直方向，一小球能在其间运动，今在最高点与最低点各放一个压力传感器，测试小球对轨道的压力，并通过计算机显示出来，当轨道距离变化时，测得两点压力差与距离x的图像如图．（g=10m／s2，不计空气阻力）求：
（1）小球的质量和半圆轨道的半径分别为多少?
（2）若x的最大值为15m，为保证小球能沿轨道运动，则小球在最底点B处的速度至少为多大?
质量为M的拖拉机拉着耙来耙地，由静止开始做匀加速直线运动，在时间t内前进的距离为s。耙地时。拖拉机受到的牵引力恒为F，受到地面的阻力为自重的k倍，耙所受阻力恒定，连接杆质量不计且与水平面的夹角θ保持不变。求：
（1）拖拉机的加速度大小。
（2）拖拉机对连接杆的拉力大小。
（3）时间t内拖拉机对耙做的功。
如图a是研究小球在斜面上平抛运动的实验装置，每次将小球从弧型轨道同一位置静止释放，并逐渐改变斜面与水平地面之间的夹角θ，获得不同的射程x，最后作出了如图b所示的x-tanθ图象，g取l0m／s2，则：
（1）由图b可知，小球在斜面顶端水平抛出时的初速度
。实验中发现θ超过60°后，小球将不会掉落在斜面上，则斜面的长度为 m。（保留1位有效数字）
（2）若最后得到的图象如图c所示，则可能的原因是 （写出一个）