如图,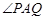 是直角,圆
是直角,圆 与射线
与射线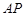 相切于点
相切于点 ,与射线
,与射线 相交于两点
相交于两点 .求证:
.求证: 平分
平分 .
.
已知函数 ,其中
,其中 为常数,且
为常数,且 。
。
(I)当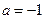 时,求
时,求 在
在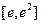 (
(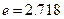
 )上的值域;
)上的值域;
(II)若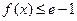 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
如图,在三棱柱 中,侧面
中,侧面 底面ABC,
底面ABC,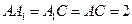 ,
,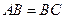 ,且
,且 为AC中点。
为AC中点。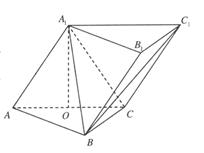
(I)证明: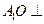 平面ABC;
平面ABC;
(II)求直线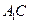 与平面
与平面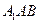 所成角的正弦值;
所成角的正弦值;
(III)在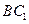 上是否存在一点E,使得
上是否存在一点E,使得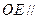 平面
平面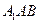 ,若不存在,说明理由;若存在,确定点E的位置。
,若不存在,说明理由;若存在,确定点E的位置。
某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.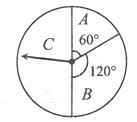
(I)若某位顾客消费128元,求返券金额不低于30元的概率;
(II)若某位顾客恰好消费280元,并按规则参与了活动,他获得返券的金额记为X(元).
求随机变量X的分布列和数学期望。
已知函数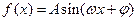 ,
,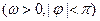 部分图像如图所示。
部分图像如图所示。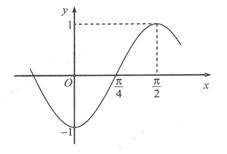
(I)求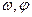 的值;
的值;
(II)设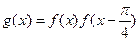 ,求函数
,求函数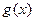 的单调递增区间。
的单调递增区间。
函数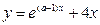
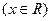 有大于零的极值点,求实数
有大于零的极值点,求实数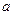 的范围
的范围