设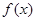 是
是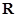 上的奇函数,当
上的奇函数,当 时,
时, ,记
,记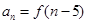 ,则数列
,则数列 的前
的前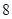 项和为 .
项和为 .
已知圆C:(x-1)2+(y-1)2=2经过椭圆Γ∶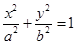 (a>b>0)的右焦点F和上顶点B.
(a>b>0)的右焦点F和上顶点B.
(1)求椭圆Γ的方程;
(2)如图,过原点O的射线l与椭圆Γ在第一象限的交点为Q,与圆C的交点为P,M为OP的中点, 求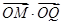 的最大值.
的最大值.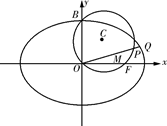
两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题,他们在沙滩上画点或用小石子来表示数,按照点或小石子能排列的形状对数进行分类,图中的实心点的个数1、5、12、22、…,被称为五角形数,其中第1个五角形数记作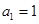 ,第2个五角形数记作
,第2个五角形数记作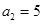 ,第3个五角形数记作
,第3个五角形数记作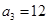 ,第4个五角形数记作
,第4个五角形数记作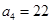 ,……,若按此规律继续下去,则
,……,若按此规律继续下去,则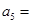 ____,若
____,若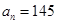 ,则
,则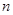 =______.
=______.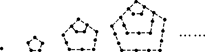
在函数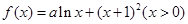 的图象上任取两个不同的点P(x1,y1)、Q(x2,y2)(
的图象上任取两个不同的点P(x1,y1)、Q(x2,y2)(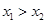 ),总能使得
),总能使得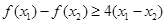 ,则实数a的取值范围为_______.
,则实数a的取值范围为_______.
若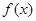 +
+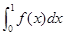 =
=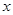 ,则
,则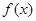 =_________.
=_________.
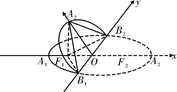
如图,椭圆 的长轴为
的长轴为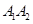 ,短轴为
,短轴为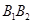 ,将坐标平面沿y轴折成一个二面角,使点
,将坐标平面沿y轴折成一个二面角,使点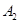 在平面
在平面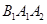 上的射影恰好是该椭圆的左焦点,则此二面角的大小为____.
上的射影恰好是该椭圆的左焦点,则此二面角的大小为____.