如图所示,在所给正方形网格图中完成下列各题:(用直尺画图,保留痕迹)
(1)求出格点△ABC(顶点均在格点上)的面积;
(2)画出格点△ABC关于直线DE对称的△A1B1C1;
(3)在DE上画出点Q,使△QAB的周长最小.
求不等式组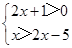 的正整数解.
的正整数解.
先化简,再求值:3(2x+1)+2(3-x),其中x=-1.
某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)加工成如图所示的竖式与横式两种无盖的长方形纸箱.(加工时接缝材料不计)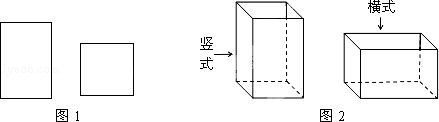
(1)该工厂原计划用若干天加工纸箱200个,后来由于对方急需要货,实际加工时每天加工速度时原计划的1.5倍,这样提前2天超额完成了任务,且总共比原计划多加工40个,问原计划每天加工纸箱多少个;
(2)若该厂购进正方形纸板1000张,长方形纸板2000张.问竖式纸盒,横式纸盒各加工多少个,恰好能将购进的纸板全部用完;
(3)该工厂某一天使用的材料清单上显示,这天一共使用正方形纸板50张,长方形纸板a张,全部加工成上述两种纸盒,且120<a<136,试求在这一天加工两种纸盒时,a的所有可能值.
如图,已知BC∥GE,AF∥DE,∠1=50°.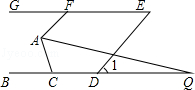
(1)求∠AFG的度数;
(2)若AQ平分∠FAC,交BC于点Q,且∠Q=15°,求∠ACB的度数.
某校为了解九年级学生体育测试情况,以九年级(1)班学生的体育测试成绩为样本,按A,B,C,D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:
(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
(1)九年级(1)班体育测试的人数为 ;
(2)请把条形统计图补充完整;
(3)扇形统计图中A级所在的扇形的圆心角度数是 ;
(4)若该校九年级有500名学生,请你用此样本估计体育测试中A级和B级的学生人数约为多少人?