如图，三棱柱
中，
平面
，
，
, 点
在线段
上，且
，
．
（Ⅰ）求证：直线
与平面不平行；
（Ⅱ）设平面
与平面所成的锐二面角为
，若
，求
的长；
（Ⅲ）在（Ⅱ）的条件下，设平面
平面
，求直线
与所成的角的余弦值．
设Sn是等差数列{an}的前n项和，已知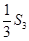
与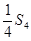
的等比中项为
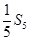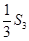，与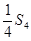的等差中项为1，求等差数列{an}的通项。
设
．
（1）判断函数y=f（x）的奇偶性；
（2）求函数y=f（x）的定义域和值域．
设关于x的函数y=2cos2x﹣2acosx﹣（2a+1）的最小值为f（a），试确定满足
的a的值，并对此时的a值求y的最大值．
设函数f（x）=sin（2x+φ）（﹣π＜φ＜0），y=f（x）图象的一条对称轴是直线
．
（I）求φ，并指出y=f（x）由y=sin2x作怎样变换所得．
（II）求函数y=f（x）的单调增区间；
（III）画出函数y=f（x）在区间[0，π]上的图象．
（1）已知tanα=2，求
+ sin2α﹣3sinα•cosα的值。
（2）已知角α终边上一点P（﹣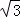
，1），求
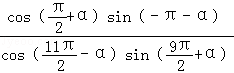的值