将一颗骰子先后抛掷2次,观察向上的点数,求:
(1)两数之和为5的概率;
(2)两数中至少有一个奇数的概率.
在平面直角坐标系 中,点P到两点(0,-
中,点P到两点(0,-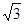 )、(0,
)、(0,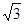 )的距离之和等于4.设点P的轨迹为C.
)的距离之和等于4.设点P的轨迹为C.
(1)写出C的方程;
(2)设直线y=kx+1与C交于A、B两点.k为何值时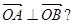 此时|
此时|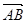 |的值是多少?
|的值是多少?
如图,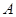 是以
是以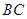 为直径的⊙O上一点,
为直径的⊙O上一点, 于点
于点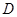 ,过点
,过点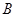 作⊙O的切线,与
作⊙O的切线,与 的延长线相交于点
的延长线相交于点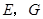 是
是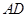 的中点,连结
的中点,连结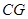 并延长与
并延长与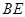 相交于点
相交于点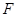 ,延长
,延长 与
与 的延长线相交于点
的延长线相交于点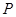 .
.
(1)求证: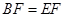 ;
;
(2) 若 , 求
, 求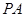 的长.
的长.
“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路 ”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,已知在这30人中随机抽取1人抽到反感“中国式过马路 ”的路人的概率是 .得到了如下列联表:
.得到了如下列联表:
| 男性 |
女性 |
合计 |
|
| 反感 |
10 |
||
| 不反感 |
8 |
||
| 合计 |
30 |
| 男性 |
女性 |
合计 |
|
| 反感 |
10 |
||
| 不反感 |
8 |
||
| 合计 |
30 |
(1)请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析是否有百分之九十五以上的把握认为反感“中国式过马路 ”与性别是否有关?
(2)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.附表
| P(K2≥k) |
0.050 |
0.010 |
0.001 |
| k |
3.841 |
6.635 |
10.828 |
如图,⊙ 的直径
的直径 的延长线与弦
的延长线与弦 的延长线相交于点
的延长线相交于点 ,
, 为⊙O上一点,弧AE等于弧AC,
为⊙O上一点,弧AE等于弧AC, 交
交 于点
于点 ,且
,且 ,求
,求 的长度.
的长度.
某班从6名班干部(其中男生4人,女生2人)中,任选3人参加学校的
义务劳动.
(1) 求男生甲或女生乙被选中的概率
(2)设“男生甲被选中”为事件A,“女生乙被选中”为事件B,求P(B)和P(A|B).